题目内容
20.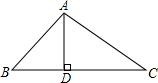 已知,如图,△ABC中,AD⊥BC于D,sinB=$\frac{\sqrt{2}}{2}$,∠C=30°,AD=3.求△ABC的周长.
已知,如图,△ABC中,AD⊥BC于D,sinB=$\frac{\sqrt{2}}{2}$,∠C=30°,AD=3.求△ABC的周长.
分析 先在Rt△ABD中根据∠B的正弦可计算出AB=$\sqrt{2}$AD=3$\sqrt{2}$,再利用勾股定理可计算出BD=3,然后在Rt△ADC中,利用∠C的正弦可计算出AC=6,则根据勾股定理可计算出CD=3$\sqrt{3}$,然后根据三角形周长的定义求解.
解答 解:在Rt△ABD中,∵sinB=$\frac{AD}{AB}$=$\frac{\sqrt{2}}{2}$,
∴AB=$\sqrt{2}$AD=3$\sqrt{2}$,
∴BD=$\sqrt{(3\sqrt{2})^{2}-{3}^{2}}$=3,
在Rt△ADC中,∵sinC=$\frac{AD}{AC}$,
∴AC=$\frac{3}{sin30°}$=6,
∴CD=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴BC=BD+CD=3+3$\sqrt{3}$,
∴△ABC的周长=AB+AC+BC=3$\sqrt{2}$+6+3+3$\sqrt{3}$=3$\sqrt{2}$+3$\sqrt{3}$+9.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活应用勾股定理和锐角三角函数的定义.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
10.已知抛物线y=ax2+bx+c与x轴交点为A(-2,0),B(6,0),则该二次函数的对称轴为( )
| A. | x=-1 | B. | x=1 | C. | x=2 | D. | y轴 |
15.如果2x+5的值与1-4x的值互为相反数,那么x等于( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
12.在半径为R的圆中,它的内接正三角形、内接正方形、内接正六边形的边长之比为( )
| A. | 1:$\sqrt{2}$:$\sqrt{3}$ | B. | $\sqrt{3}$:$\sqrt{2}$:1 | C. | 1:2:3 | D. | 3:2:1 |
 如图,直线AB、CD相交与点O,OE是∠AOD的平分线,∠AOC=26°,求:
如图,直线AB、CD相交与点O,OE是∠AOD的平分线,∠AOC=26°,求: 如图,沿所画线折叠能形成一个立体图形,它的名称是三棱柱.
如图,沿所画线折叠能形成一个立体图形,它的名称是三棱柱.