题目内容
10.已知抛物线y=ax2+bx+c与x轴交点为A(-2,0),B(6,0),则该二次函数的对称轴为( )| A. | x=-1 | B. | x=1 | C. | x=2 | D. | y轴 |
分析 根据抛物线的对称性得到点A和点B是抛物线上的对称点,所以点A和点B的对称轴即为抛物线的对称轴.
解答 解:∵抛物线y=ax2+bx+c与x轴交点为A(-2,0),B(6,0),
∴该二次函数的对称轴为直线x=2.
故选C.
点评 本题考查了抛物线与x轴的交点:从二次函数的交点式y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)中可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).解决本题的关键是掌握抛物线的对称性.

练习册系列答案
相关题目
10.小王第一天做了x个零件,第二天比第一天多做5个,第三天做的零件是第二天的2倍,若三天共做零件75个,则第一天做了( )个.
| A. | 15 | B. | 14 | C. | 10 | D. | 20 |
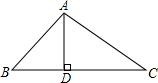 已知,如图,△ABC中,AD⊥BC于D,sinB=$\frac{\sqrt{2}}{2}$,∠C=30°,AD=3.求△ABC的周长.
已知,如图,△ABC中,AD⊥BC于D,sinB=$\frac{\sqrt{2}}{2}$,∠C=30°,AD=3.求△ABC的周长.