题目内容
20.甲、乙两名运动员进行长袍训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数图象如图1所示(甲为线段AB,乙为折线ACB),根据图象所提供的信息解答问题:
(1)他们在进行5000米的长跑训练,甲的速度是250米/分,乙前15分钟的速度是200米/分;
(2)分别求甲、乙距终点的路程y(米)与跑步时间x(分)之间的函数关系式;
(3)试求x为何值时,两人相距100米?
(4)若设甲乙两人之间的距离为s(米),试根据题意在图2所示的坐标系中绘制出s(米)与跑步时间t(分)之间的函数图象.
分析 (1)由函数图象可以得到他们进行的是多少米的长跑训练和甲的速度和乙前15分钟的速度分别是多少;
(2)根据函数图象分别设出各段的函数解析式,根据函数图象中的数据可以求出各段的函数解析式;
(3)由题意可以知道两人相距100米有两种情况,分别写出相应的关系式即可解答本题;
(4)画出相应的函数图象关键是求出15钟时两人相距最远,算出这个最远距离,从而可以画出相应的函数图象.
解答 解:(1)由图象可得,
他们在进行5000米的长跑训练,甲20分钟跑了5000米,乙前15分钟跑了(5000-2000)米,
则甲的速度为:5000÷20=250米/分,乙的速度为:3000÷15=200米/分,
故答案为:5000,250米/分,200米/分;
(2)设线段AC对应的函数解析式为:y=kx+b,
则$\left\{\begin{array}{l}{b=5000}\\{20k+b=0}\end{array}\right.$
解得k=-250,b=5000,
∴线段AC对应的函数解析式是:y=-250x+5000(0≤x≤20);
设线段AB对应的函数解析式为:y=mx+n,
则$\left\{\begin{array}{l}{n=5000}\\{15m+n=2000}\end{array}\right.$
解得,m=-200,n=5000,
∴线段AB对应的函数解析式是:y=-200x+5000(0≤x≤15),
设线段BC对应的函数解析式为:y=ax+c,
则$\left\{\begin{array}{l}{15a+c=2000}\\{20a+c=0}\end{array}\right.$
解得,a=-400,c=8000,
∴线段BC对应的函数解析式是:y=-400x+8000(15<x≤20);
由上可得,甲距终点的路程y(米)与跑步时间x(分)之间的函数关系式是:y=-250x+5000(0≤x≤20);
乙距终点的路程y(米)与跑步时间x(分)之间的函数关系式是:y=$\left\{\begin{array}{l}{-200x+5000}&{(0≤x≤15)}\\{-400x+8000}&{(15<x≤20)}\end{array}\right.$;
(3)由题意可得,
-200x+5000-(-250x+5000)=100或-400x+8000-(-250x+5000)=100,
解得,x=2或x=$\frac{58}{3}$,
即当x=2或x=$\frac{58}{3}$,两人相距100米;
(4)由题意和函数图象可得,
当x=15时,两人相距最远,最远的距离为:-200×15+5000-(-250×15+5000)=750米,
故s(米)与跑步时间t(分)之间的函数图象如下图2所示: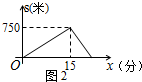 .
.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件即可.


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | -2015 | B. | 2015 | C. | -1 | D. | 1 |
| A. | -1 | B. | 8 | C. | 2 | D. | -2 |
 如图,DA=DE,∠ADE=90°,C为DE延长线上一点,AB⊥AC,且AB=AC,延长AD交BE于F.
如图,DA=DE,∠ADE=90°,C为DE延长线上一点,AB⊥AC,且AB=AC,延长AD交BE于F.