题目内容
4.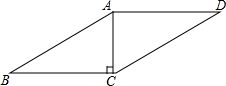 如图,在?ABCD中,过A点作高,垂足刚好为点C,AB=4,AC=2,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AB=4,AC=2,则?ABCD的周长是( )| A. | 8+4$\sqrt{3}$ | B. | 4+2$\sqrt{3}$ | C. | 8 | D. | 4 |
分析 根据含30°角的直角三角形的性质,求出BC,再根据平行四边形的性质求得结果.
解答 解:在Rt△ABD中,
∵AB=4,AC=2,即AC=$\frac{1}{2}$AB,
∴∠B=30°,
∴BC=2$\sqrt{3}$,
∵?ABCD,
∴AB=CD,AD=BC,
∴?ABCD的周长=2(AB+BC)=8+4$\sqrt{3}$,
故选A
点评 本题主要考查了含30°角的直角三角形的性质,平行四边形的性质,能灵活应用这两个性质是解题的关键.

练习册系列答案
相关题目
15.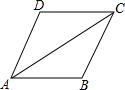 如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为( )
如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为( )
 如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为( )
如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
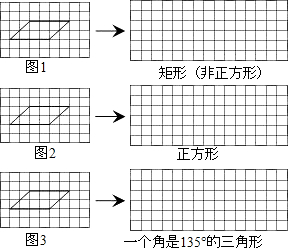 分别在图1、图2、图3中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,并把折两部分重新拼成符合下列要求的几何图形.
分别在图1、图2、图3中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,并把折两部分重新拼成符合下列要求的几何图形.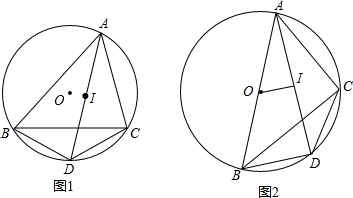
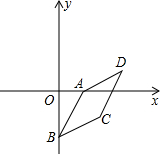 如图:在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移到BC,使B(0,b),且a,b满足|2-a|+$\sqrt{6+b}$=0
如图:在平面直角坐标系中,A(a,0),D(6,4),将线段AD平移到BC,使B(0,b),且a,b满足|2-a|+$\sqrt{6+b}$=0