题目内容
正比例函数y=mx的图象与反比例函数y=
的图象有公共点,则mk= .
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:分两种情况分别分析,根据正比例函数和反比例函数的性质即可求得.
解答:解:若m>0,则正比例函数y=mx的图象经过一、三象限,
∵正比例函数y=mx的图象与反比例函数y=
的图象有公共点,
∴反比例函数y=
的图象也在一、三象限,
∴k>0,
∴km>0;
若m<0,则正比例函数y=mx的图象经过二、四象限,
∵正比例函数y=mx的图象与反比例函数y=
的图象有公共点,
∴反比例函数y=
的图象也在二、四象限,
∴k<0,
∴km>0;
所以km>0,
故答案为>.
∵正比例函数y=mx的图象与反比例函数y=
| k |
| x |
∴反比例函数y=
| k |
| x |
∴k>0,
∴km>0;
若m<0,则正比例函数y=mx的图象经过二、四象限,
∵正比例函数y=mx的图象与反比例函数y=
| k |
| x |
∴反比例函数y=
| k |
| x |
∴k<0,
∴km>0;
所以km>0,
故答案为>.
点评:本题考查的是正比例函数与反比例函数的交点问题,熟知正比例函数与反比例函数的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在实数1.414,π,2+
,
,-
,0.101001000…中,无理数有( )
| 3 |
| 3 | 9 |
| 2 |
| A、3个 | B、4个 | C、5个 | D、6个 |
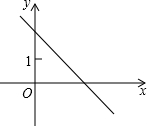 如图,直线l:y=-x+b,点M(3,2)关于直线l的对称点M1落在y轴上,则b的值等于( )
如图,直线l:y=-x+b,点M(3,2)关于直线l的对称点M1落在y轴上,则b的值等于( )| A、3 | B、2 | C、1或2 | D、2或3 |
 如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.
如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度. 已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.
已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.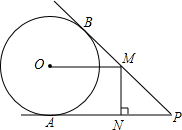 如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.