题目内容
如图1,AB是半⊙O的直径,过A、B两点作半⊙O的弦,当两弦交点恰好落在半⊙O上C点时,则有AC•AC+BC•BC=AB2
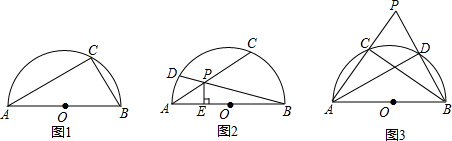
(1)如图2,若两弦交于点P在半⊙O内,则AP•AC+BP•BD=AB2是否成立?请说明理由;
(2)如图3,若两弦AC、BD的延长线交于P点,则AB2= .参照(1)填写相应的,并证明你填写结论的正确性.

(1)如图2,若两弦交于点P在半⊙O内,则AP•AC+BP•BD=AB2是否成立?请说明理由;
(2)如图3,若两弦AC、BD的延长线交于P点,则AB2=
考点:圆的综合题
专题:综合题
分析:(1)连结AD、BC,作PE⊥AB于E,如图2,根据圆周角定理由AB为直径得到∠D=∠C=90°,再由OE⊥AB得到∠PEA=∠PEB=90°,则可判断点A、E、P、D四点共圆;点B、E、P、C四点共圆,根据切割线定理得到BE•BA=BP•BD,AE•AB=AP•AC,把两式相加得AP•AC+BP•BD=AE•AB+BE•BA=AB(AE+BE)=AB2;
(2)BC与AD相交于E,如图3,根据圆周角定理得∠ADB=∠ACB=90°,则点C、E、D、P四点共圆,根据切割线定理得到BE•BC=BP•BD,AE•AD=AP•AC,则AP•AC+BP•BD=AE•AD+BE•BC,然后利用(1)的结论即可得到AB2=AP•AC+BP•BD.
(2)BC与AD相交于E,如图3,根据圆周角定理得∠ADB=∠ACB=90°,则点C、E、D、P四点共圆,根据切割线定理得到BE•BC=BP•BD,AE•AD=AP•AC,则AP•AC+BP•BD=AE•AD+BE•BC,然后利用(1)的结论即可得到AB2=AP•AC+BP•BD.
解答:解:(1)成立.理由如下:
连结AD、BC,作PE⊥AB于E,如图2,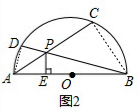
∵AB为直径,
∴∠D=∠C=90°,
∵OE⊥AB,
∴∠PEA=∠PEB=90°,
∴点D、E在以AP为直径的圆上,即点A、E、P、D四点共圆;点C、E在以BP为直径的圆上,即点B、E、P、C四点共圆,
∴BE•BA=BP•BD,AE•AB=AP•AC,
∴AP•AC+BP•BD=AE•AB+BE•BA=AB(AE+BE)=AB•AB=AB2;
(2)AB2=AP•AC+BP•BD.理由如下: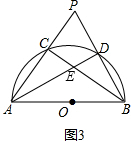
BC与AD相交于E,如图3,
∵AB为直径,
∴∠ADB=∠ACB=90°,
∴点C、E、D、P四点共圆,
∴BE•BC=BP•BD,AE•AD=AP•AC,
∴AP•AC+BP•BD=AE•AD+BE•BC,
由(1)的结论得AE•AD+BE•BC=AB2,
∴AB2=AP•AC+BP•BD.
故答案为AP•AC+BP•BD.
连结AD、BC,作PE⊥AB于E,如图2,

∵AB为直径,
∴∠D=∠C=90°,
∵OE⊥AB,
∴∠PEA=∠PEB=90°,
∴点D、E在以AP为直径的圆上,即点A、E、P、D四点共圆;点C、E在以BP为直径的圆上,即点B、E、P、C四点共圆,
∴BE•BA=BP•BD,AE•AB=AP•AC,
∴AP•AC+BP•BD=AE•AB+BE•BA=AB(AE+BE)=AB•AB=AB2;
(2)AB2=AP•AC+BP•BD.理由如下:

BC与AD相交于E,如图3,
∵AB为直径,
∴∠ADB=∠ACB=90°,
∴点C、E、D、P四点共圆,
∴BE•BC=BP•BD,AE•AD=AP•AC,
∴AP•AC+BP•BD=AE•AD+BE•BC,
由(1)的结论得AE•AD+BE•BC=AB2,
∴AB2=AP•AC+BP•BD.
故答案为AP•AC+BP•BD.
点评:本题考查了圆的综合题:熟练掌握圆周角定理、四点共圆的判定方法和切割线定理;学会由特殊到一般的解决问题的思想方法.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
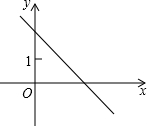 如图,直线l:y=-x+b,点M(3,2)关于直线l的对称点M1落在y轴上,则b的值等于( )
如图,直线l:y=-x+b,点M(3,2)关于直线l的对称点M1落在y轴上,则b的值等于( )| A、3 | B、2 | C、1或2 | D、2或3 |
 如图,直线a∥b,则∠A的度数是
如图,直线a∥b,则∠A的度数是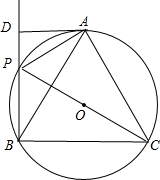
 如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.
如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.