题目内容
6.解方程:(1)$\frac{1}{x-2}$+$\frac{2x}{x+2}$=2-$\frac{1-x}{{x}^{2}-4}$
(2)($\frac{27}{8}$)x-1×($\frac{2}{3}$)2x-3=$\frac{4}{9}$.
分析 (1)两边同时乘以最简公分母(x+2)(x-2),解出x的值,千万不要忘记检验;
(2)将方程的两边化为同底数幂,根据同底数幂的乘法法则,得到关于x的一元一次方程,解方程即可.
解答 解:(1)两边同时乘以(x+2)(x-2),得:
(x+2)+2x(x-2)=2(x+2)(x-2)-(1-x),
解得:x=$\frac{11}{4}$,
检验:把x=$\frac{11}{4}$代入(x+2)(x-2)≠0,
∴x=$\frac{11}{4}$是原分式方程的解;
(2)原方程可化为:($\frac{3}{2}$)3(x-1)×($\frac{2}{3}$)(2x-3)=($\frac{2}{3}$)2,
($\frac{2}{3}$)-3(x-1)×($\frac{2}{3}$)(2x-3)=($\frac{2}{3}$)2,
即-3(x-1)+(2x-3)=2,
解得:x=-2.
点评 本题主要考查解分式方程,解分式方程时必须检验,解决第(2)小题时,将其化为同底数幂是解题的关键.

练习册系列答案
相关题目
16.小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬按20元/小时计算,设小明得哥哥这个月的工作时间为t(小时),应得报酬为m(元),请填写下表,然后回答下面问题
(1)你能用含t的代数式表示m的值吗?
(2)在上述问题中,那些是常量?那么是变量?
| 工作时间t(小时) | 1 | 5 | 10 | 15 | 20 | … | t | … |
| 报酬m(元) | 20 | 100 | 200 | 300 | 400 | … | 20t | … |
(2)在上述问题中,那些是常量?那么是变量?
16.二次根式$\sqrt{2x-1}$中字母x可以取的数是( )
| A. | 0 | B. | 2 | C. | -$\sqrt{3}$ | D. | -1 |
 如图,△ABC中,∠BAC=45°,过A、B两点的⊙O交AC于点D,且OD∥BC,OD交AB于点E.
如图,△ABC中,∠BAC=45°,过A、B两点的⊙O交AC于点D,且OD∥BC,OD交AB于点E.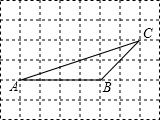 如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)
如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点) 以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点,
以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点, 如图,在线段BF上,有点E、C,BE=CF,∠B=∠F,∠ACB=∠DEF.
如图,在线段BF上,有点E、C,BE=CF,∠B=∠F,∠ACB=∠DEF.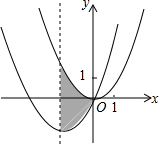 如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.
如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.