Question

14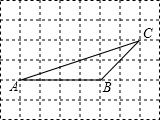．如图，在方格纸中，点A、B、C是三个格点（网格线的交点叫做格点）
（1）过点C画AB的垂线，垂足为D；
（2）将点D沿BC翻折，得到点E，作直线CE；
（3）直线CE与直线AB的位置关系是平行；
（4）判断：∠ACB＞∠ACE．（填“＞”、“＜”或“=”

Answer 1

分析 （1）直接利用网格结合垂直的定义得出D点位置；
（2）直接利用翻折变换的性质得出E点位置；
（3）利用网格得出直线CE与直线AB的位置关系；
（4）利用同一三角形中大角对大边得出答案．

解答 解：（1）如图所示：点D即为所求；

（2）如图所示：直线EC，即为所求；

（3）直线CE与直线AB的位置关系是：平行；
故答案为：平行；

（4）如图所示：∵∠ECA=∠A，AB＞BC，
∴∠ACB＞∠A，
∴∠ACB＞∠ACE．
故答案为：＞．

点评 此题主要考查了基本作图以及轴对称变换，正确借助网格分析是解题关键．