题目内容
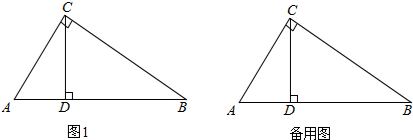
如图，∠AOB=45°，点O1在OA上，OO1=7，⊙O1的半径为2，点O2在射线OB上运动，且⊙O2始终与OA相切，当⊙O2和⊙O1相切时，⊙O2的半径等于考点：圆与圆的位置关系
专题：压轴题,数形结合
分析：作O2C⊥OA于点C，连接O1O2，设O2C=r，根据⊙O1的半径为2，OO1=7，表示出O1O2=r+2，O1C=7-r，利用勾股定理列出有关r的方程求解即可．
解答：解：如图，作O2C⊥OA于点C，连接O1O2，
设O2C=r，
∵∠AOB=45°，
∴OC=O2C=r，
∵⊙O1的半径为2，OO1=7，
∴O1O2=r+2，O1C=7-r，
∴（7-r）2+r2=（r+2）2，
解得：r=3或15，
故答案为：3或15．
设O2C=r，
∵∠AOB=45°，
∴OC=O2C=r，
∵⊙O1的半径为2，OO1=7，
∴O1O2=r+2，O1C=7-r，
∴（7-r）2+r2=（r+2）2，
解得：r=3或15，
故答案为：3或15．
点评：本题考查了圆与圆的位置关系，解题的关键是正确的作出图形，难度中等．
练习册系列答案
相关题目
平行四边形ABCD在平面直角坐标系中的位置如图所示，其中点A（-4，0），B（2，0），C（3，3）．反比例函数y=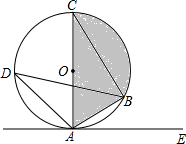
如图，AC是⊙O的直径，点B，D在⊙O上，点E在⊙O外，∠EAB=∠D=30°．
如图，已知在Rt△OAC中，O为坐标原点，直角顶点C在x轴的正半轴上，反比例函数y=