题目内容
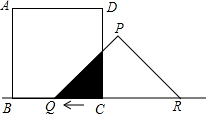 已知有一边为5cm的正方形ABCD和等腰三角形PQR,PQ=PR=5cm,QR=5
已知有一边为5cm的正方形ABCD和等腰三角形PQR,PQ=PR=5cm,QR=5| 2 |
(1)t秒后正方形ABCD与等腰三角形PQR重合部分的面积为5,求时间t;
(2)当正方形ABCD与等腰三角形PQR重合部分的面积为7,求时间t.
考点:一元二次方程的应用
专题:几何动点问题
分析:在等腰三角形PQR中,由PQ=PR=5cm,QR=5
cm,根据勾股定理的逆定理可得,等腰三角形PQR是等腰直角三角形,进而得到三角形ECQ是等腰直角三角形,然后根据三角形的面积公式即可求解.
| 2 |
解答:解:在等腰三角形PQR中,
∵PQ=PR=5cm,QR=5
cm,
∴PQ2+PR2=52+52=50=(5
)2=QR2,
∴等腰三角形PQR是等腰直角三角形.
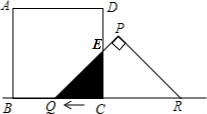
(1)当正方形ABCD与等腰三角形PQR重合部分的面积为5时,
即S△ECQ=5cm2,
由题意知,△ECQ是等腰直角三角形,
∴EC=QC=t,
∵S△ECQ=
EC•QC=5,\
即
t2=5,
解得:t1=
,t2=-
(舍去),
∴
秒后正方形ABCD与等腰三角形PQR重合部分的面积为5.
(2)当正方形ABCD与等腰三角形PQR重合部分的面积为7时,
同(1)可得
t2=7,
解得:t1=
,t2=-
(舍去),
∴
秒后正方形ABCD与等腰三角形PQR重合部分的面积为7.
∵PQ=PR=5cm,QR=5
| 2 |
∴PQ2+PR2=52+52=50=(5
| 2 |
∴等腰三角形PQR是等腰直角三角形.
(1)当正方形ABCD与等腰三角形PQR重合部分的面积为5时,
即S△ECQ=5cm2,
由题意知,△ECQ是等腰直角三角形,
∴EC=QC=t,
∵S△ECQ=
| 1 |
| 2 |
即
| 1 |
| 2 |
解得:t1=
| 10 |
| 10 |
∴
| 10 |
(2)当正方形ABCD与等腰三角形PQR重合部分的面积为7时,
同(1)可得
| 1 |
| 2 |
解得:t1=
| 14 |
| 14 |
∴
| 14 |

点评:此题考查了一元二次方程的应用、正方形的性质、等腰三角形的性质、图形面积的求法等知识,由勾股定理的逆定理判断直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,矩形ABCD的两条对角线交于点O,若∠AOD=120°,AB=6,则AC等于( )
如图,矩形ABCD的两条对角线交于点O,若∠AOD=120°,AB=6,则AC等于( )| A、8 | B、10 | C、12 | D、18 |
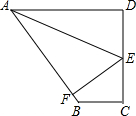 如图,AD∥BC,CD⊥AD,AE平分∠BAD,且E是DC的中点,EF⊥AB于点F,判断AD、BC与AB之间的数量关系并说明理由.
如图,AD∥BC,CD⊥AD,AE平分∠BAD,且E是DC的中点,EF⊥AB于点F,判断AD、BC与AB之间的数量关系并说明理由.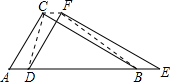 如图,△ABC中,∠ACB=90°,∠A=60°,AC=2.将△ABC沿射线AB向右平移得到△DEF,连接DC、CF、FB,在平移的过程中,有以下结论:①四边形ADFC始终是平行四边形;②以C、D、B、F为顶点的四边形面积始终等于2
如图,△ABC中,∠ACB=90°,∠A=60°,AC=2.将△ABC沿射线AB向右平移得到△DEF,连接DC、CF、FB,在平移的过程中,有以下结论:①四边形ADFC始终是平行四边形;②以C、D、B、F为顶点的四边形面积始终等于2 如图,在△ABC中,∠BAC是钝角,请画出AB边上的高CD,BC边上的中线AE,并将△ABC沿AE方向平移AE的长度.(请保留作图痕迹,并写出结论)
如图,在△ABC中,∠BAC是钝角,请画出AB边上的高CD,BC边上的中线AE,并将△ABC沿AE方向平移AE的长度.(请保留作图痕迹,并写出结论)