题目内容
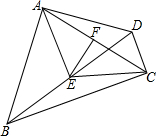 如图所示,四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是BD,AC的中点.
如图所示,四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是BD,AC的中点.(1)求证:AE=CE;
(2)判断EF与AC的位置关系,并说明理由.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得AE=
BD,CE=
BD,即可得证;
(2)根据等腰三角形三线合一的性质解答.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据等腰三角形三线合一的性质解答.
解答:(1)证明:∵∠BAD=∠BCD=90°,E是BD的中点,
∴AE=
BD,CE=
BD,
∴AE=CE;
(2)解:EF⊥AC.
理由如下:∵AE=CE,点F是AC的中点,
∴EF⊥AC.
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=CE;
(2)解:EF⊥AC.
理由如下:∵AE=CE,点F是AC的中点,
∴EF⊥AC.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
自我县开展“创建省级园林城市 建设生态宜居阜宁”活动以来,学生更加自觉遵守交通规则.中学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为
,遇到黄灯的概率为
,那么他遇到绿灯的概率为( )
| 1 |
| 3 |
| 1 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若点P(a,b)在第四象限内,则a,b的取值范围是( )
| A、a>0,b<0 |
| B、a>0,b>0 |
| C、a<0,b>0 |
| D、a<0,b<0 |
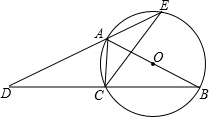 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC、CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC、CE. 如图,若∠1=∠D,BD平分∠ABC,且∠ABC=55°,试求∠BCD的度数.
如图,若∠1=∠D,BD平分∠ABC,且∠ABC=55°,试求∠BCD的度数.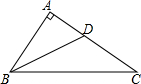 如图,在△ABC中,∠A=90°,BD是角平分线,若AD=m,BC=n,求△BCD的面积.
如图,在△ABC中,∠A=90°,BD是角平分线,若AD=m,BC=n,求△BCD的面积.