题目内容
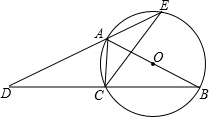 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC、CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC、CE.(1)求证:∠B=∠D;
(2)若AB=13,BC-AC=7,求CE的长.
考点:圆周角定理
专题:
分析:(1)由AB为⊙O的直径,易证得AC⊥BD,又由DC=CB,根据线段垂直平分线的性质,可证得AD=AB,即可得:∠B=∠D;
(2)首先设BC=x,则AC=x-7,由在Rt△ABC中,AC2+BC2=AB2,可得方程:(x-7)2+x2=132,解此方程即可求得CB的长,继而求得CE的长.
(2)首先设BC=x,则AC=x-7,由在Rt△ABC中,AC2+BC2=AB2,可得方程:(x-7)2+x2=132,解此方程即可求得CB的长,继而求得CE的长.
解答:(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x-7,
在Rt△ABC中,AC2+BC2=AB2,
即(x-7)2+x2=132,
解得:x1=12,x2=-5(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=12.
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x-7,
在Rt△ABC中,AC2+BC2=AB2,
即(x-7)2+x2=132,
解得:x1=12,x2=-5(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=12.
点评:此题考查了圆周角定理、线段垂直平分线的性质、等腰三角形的判定与性质以及勾股定理等知识.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
(-1)2n+1+(-1)2n=( )(n为正整数)
| A、2 | B、-2 | C、2或-2 | D、0 |
一个正方形的面积为17,估计它的边长大小为( )
| A、2与3之间 |
| B、3与4之间 |
| C、4与5之间 |
| D、5与6之间 |
 在平面直角坐标系xOy中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C,若m=2,n=1,求A、B两点的坐标.
在平面直角坐标系xOy中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C,若m=2,n=1,求A、B两点的坐标. 图中∠B的同旁内角有几个?分别是由哪两条直线被哪一条直线所截而成的?
图中∠B的同旁内角有几个?分别是由哪两条直线被哪一条直线所截而成的?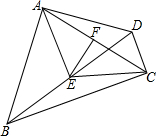 如图所示,四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是BD,AC的中点.
如图所示,四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是BD,AC的中点.