题目内容
9.化简:($\frac{{2{a^2}+2a}}{{{a^2}-1}}$-$\frac{{{a^2}-a}}{{{a^2}-2a+1}}}$)÷$\frac{2a}{a-1}$.分析 根据分式的减法和除法可以解答本题.
解答 解:($\frac{{2{a^2}+2a}}{{{a^2}-1}}$-$\frac{{{a^2}-a}}{{{a^2}-2a+1}}}$)÷$\frac{2a}{a-1}$
=$[{\frac{{2a({a+1})}}{{({a+1})({a-1})}}-\frac{{a({a-1})}}{{{{({a-1})}^2}}}}]÷\frac{2a}{a-1}$
=$({\frac{2a}{a-1}-\frac{a}{a-1}})÷\frac{2a}{a-1}$
=$\frac{a}{a-1}÷\frac{2a}{a-1}$
=$\frac{a}{a-1}•\frac{a-1}{2a}$
=$\frac{1}{2}$.
点评 本题考查分式的混合运算,解答本题的关键是明确分式的混合运算的计算方法.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
20.小明的身高不低于1.7米,设身高为h米,用不等式可表示为( )
| A. | h>1.7 | B. | h<17 | C. | h≤1.7 | D. | h≥1.7 |
1.m是常数,若不等式组$\left\{\begin{array}{l}{x<1}\\{x>m-1}\end{array}\right.$恰有两个整数解,则m的值可能是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
7.为了了解2015年我市七年级学生期末考试的数学成绩,从中随机抽取了1000名学生的数学成绩进行分析,下列说法错误的是( )
| A. | 2015年我市七年级学生期末考试的数学成绩是总体 | |
| B. | 样本容量是1000名 | |
| C. | 1000名七年级学生期末考试的数学成绩是总体的一个样本 | |
| D. | 每一名七年级学生期末考试的数学成绩是个体 |
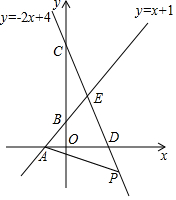 如图,直线y=x+1与x,y轴交于点A,B,直线y=-2x+4与x、y轴交于点D,C,这两条直线交于点E.
如图,直线y=x+1与x,y轴交于点A,B,直线y=-2x+4与x、y轴交于点D,C,这两条直线交于点E. 如图,从数轴的原点O向右数出3个单位,记为点A,过点A作数轴的垂线并截取AB为1个单位长度,连接OB,以点O为圆心,以OB为半径画弧,交数轴的正半轴于点C,则点C所表示的实数为$\sqrt{10}$.
如图,从数轴的原点O向右数出3个单位,记为点A,过点A作数轴的垂线并截取AB为1个单位长度,连接OB,以点O为圆心,以OB为半径画弧,交数轴的正半轴于点C,则点C所表示的实数为$\sqrt{10}$.