Question

15．如图，在四边形ABCD中，∠ABC=∠DCB，AB=CD，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF=DE，连接BF、CF、AC．
（1）求证：四边形ABFC是平行四边形；
（2）若DE²=BE•CE，求证：四边形ABFC是矩形．

Answer 1

分析 （1）连接BD，利用等腰梯形的性质得到AC=BD，再根据垂直平分线的性质得到DB=FB，从而得到AC=BF，然后证得AC∥BF，即可得出结论；
（2）利用题目提供的等积式和两直角相等可以证得两直角三角形相似，得到对应角相等，从而得到直角来证明有一个角是直角的平行四边形是矩形．

解答 （1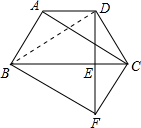）证明：连接BD，如图所示：
∵梯形ABCD中，AD∥BC，AB=CD，
∴AC=BD，
∵DE⊥BC，EF=DE，
∴BD=BF，CD=CF，
∴AC=BF，AB=CF，
∴四边形ABFC是平行四边形；
（2）证明：∵DE²=BE•CE，
∴$\frac{DE}{CE}=\frac{BE}{DE}$，
∵∠DEB=∠DEC=90°，
∴△BDE∽△DCE，
∴∠CDE=∠DBE，
∴∠BFC=∠BDC=∠BDE+∠CDE=∠BDE+∠DBE=90°，
∴四边形ABFC是矩形．

点评 本题考查了等腰梯形的性质、全等及相似三角形的判定及性质等，是一道集合了好几个知识点的综合题，但题目的难度不算大．