题目内容
1. 如图,△ABC内接于⊙O,AD交BC于点D,点P是$\widehat{BC}$的中点,求证:AP平分∠OAD.
如图,△ABC内接于⊙O,AD交BC于点D,点P是$\widehat{BC}$的中点,求证:AP平分∠OAD.
分析 连接OP,如图,利用角平分线的定义得到∠BAP=∠CAP,则根据圆周角定理得弧BP=弧CP,于是可根据垂径定理得到OP⊥BC,易得OP∥AD,根据平行线的性质得∠P=∠2,加上∠1=∠P,所以∠1=∠2.
解答  证明:连接OP,如图,
证明:连接OP,如图,
∵点P是$\widehat{BC}$的中点,
∴AP平分∠BAC,
∴∠BAP=∠CAP,
∴弧BP=弧CP,
∴OP⊥BC,
又∵AD⊥BC,
∴OP∥AD,
∴∠P=∠2,
∵OA=OP,
∴∠1=∠P,
∴∠1=∠2,
即AP平分∠DAO.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.

练习册系列答案
相关题目
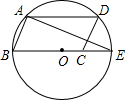 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=70°,连接
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=70°,连接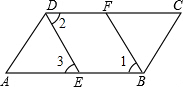 已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC.且∠1=∠3.
已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC.且∠1=∠3. 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为24.
如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为24.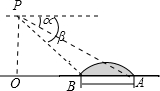 如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m)
如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m)