题目内容
16．
如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分，当菱形的两条对角线的长分别为12和8时，则阴影部分的面积为24．
分析 根据菱形的面积等于对角线乘积的一半求出面积，再根据中心对称的性质判断出阴影部分的面积等于菱形的面积的一半，即可得出结果．
解答 解：如图所示：
∵菱形ABCD的两条对角线的长分别为12和8，
∴菱形ABCD的面积=$\frac{1}{2}$×12×8=48，
∵O是菱形两条对角线的交点，菱形ABCD是中心对称图形，
∴△OEG≌△OFH，四边形OMAH≌四边形≌四边形ONCG，四边形OEDM≌四边形OFBN，
∴阴影部分的面积=$\frac{1}{2}$S菱形ABCD=$\frac{1}{2}$×48=24．
故答案为：24．
点评 本题考查了中心对称、菱形的性质；熟记菱形的性质并判断出阴影部分的面积等于菱形的面积的一半是解题的关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
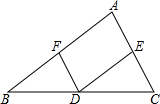如图，已知DE∥AB，DF∥AC，∠EDC=32°，∠BDF=63°，求∠A的度数；
如图，△ABC内接于⊙O，AD交BC于点D，点P是$\widehat{BC}$的中点，求证：AP平分∠OAD．
某校对200名学生进行“最爱看电视节目”调查，得到如图扇形统计图，其中最爱看文艺类节目的学生有80人．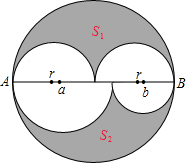
如图，大圆的半径为r，直径AB上方两个半圆的直径均为r，下方两个半圆的直径分别为a，b．