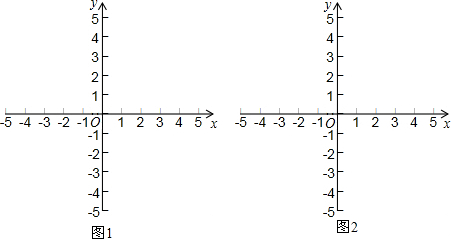题目内容
8．
已知数a、b、c在数轴上的位置如图所示，化简|a+b|-|a-b|+|a+c|．
分析 先根据题意得出a、b、c的取值范围，再得出a+b，a-b＜，a+c的正负性，根据绝对值的性质求出各式的绝对值，化简合并即可．
解答 解：根据题意得：-2＜c＜0，0＜a＜1，2＜b＜3，
∴a+b＞0，a-b＜0，a+c＜0，
∴原式=a+b-[-（a-b）]+[-（a+c）]
=a+b+a-b-a-c
=a-c．
点评 本题考查了数轴、绝对值以及整式的加减；熟练掌握绝对值的性质得出各式的绝对值是解决问题的关键．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
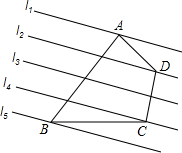如图，已知直线l1∥l2∥l3∥l4∥l5，相邻两条平行直线间的距离相等且为1，如果四边形ABCD的四个顶点在平行直线上，∠BAD=90°且AB=3AD，DC⊥l4，则四边形ABCD的面积是$\frac{17}{2}$．
13．若a=$\frac{1}{\sqrt{2}}$，b=$\frac{\sqrt{2}}{2}$，则（ ）
| A． | a=b | B． | a、b互为倒数 | C． | ab=2 | D． | a、b互为相反数 |
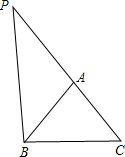在△ABC中，AB=6，BC=8，CA=7，延长CA至点P，使∠PBA=∠C，则AP=9．