题目内容
2.如图1,数学课上,杨老师拿出一张菱形纸片ABCD.对角线AC、BD相交于点O.(1)老师沿着AC剪一刀,让小明把剪开的两部分拼成一个平行四边形,在图2中用实线画出小明所拼成的平行四边形;
(2)老师又沿着BD剪开,让小彬把剪开的两部分拼成一个平行四边形,在图3中用实线画出小明所拼成的
平行四边形;
(3)老师再次沿着某条直线剪开,拼成与上述两种都不相同的平行四边形,请在图4中用实线画出老师拼成
的平行四边形;
(4)在图1的菱形纸片ABCD中,若 AC=8cm,BD=6cm.求出这个菱形的周长和面积.

分析 (1)(2)(3)根据题意画出图形即可;
(4)由菱形的性质得出AO=CO,BO=DO,AC⊥BD,AB=BC=CD=DA,由勾股定理求出AB,得出菱形的周长;菱形ABCD的面积=$\frac{1}{2}AC$•BD,代入计算即可.
解答 解:(1)(2)(3)如图所示: (4)∵菱形ABCD的对角线AC、BD相交于点O.
(4)∵菱形ABCD的对角线AC、BD相交于点O.
∴AO=CO,BO=DO,AC⊥BD,AB=BC=CD=DA,
∵AC=8cm,BD=6cm,
∴AO=4cm,BO=3cm,
∴AB=$\sqrt{{4}^{2}+{3}^{2}}$=5cm,
∴菱形ABCD的周长=4×5cm=20cm,
菱形ABCD的面积=$\frac{1}{2}AC$•BD=$\frac{1}{2}×8×6=24$cm2.
点评 本题考查了图形的剪拼、平行四边形的性质、菱形的性质、勾股定理等知识;熟练掌握平行四边形和菱形的性质,由勾股定理求出AB是解决问题(4)的关键.

练习册系列答案
相关题目
20.下列运算正确的是( )
| A. | $\sqrt{4}$=2 | B. | (-3)2=-9 | C. | $\sqrt{25}$=±5 | D. | $\root{3}{-8}$=2 |
7.已知$\left\{\begin{array}{l}{3x+2t=4}\\{2y-t=3}\end{array}\right.$,则用含x的代数式表示y为y=$\frac{-3x+10}{4}$.
14.下列各组数是三角形的三边,能组成直角三角形的一组数是( )
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 2,3,4 | C. | 3,4,5 | D. | 6,8,12 |
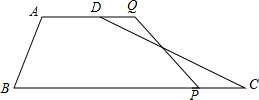 如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q.
如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q. 如图,△ABC的三个顶点分别为A(1,1)、B(4,2)、C(3,4).
如图,△ABC的三个顶点分别为A(1,1)、B(4,2)、C(3,4).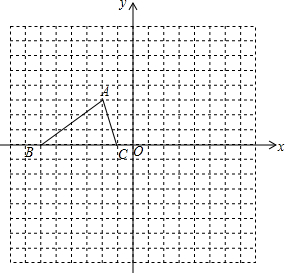 如图,已知△ABC的三个顶点坐标为A(-2,3),B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点坐标为A(-2,3),B(-6,0),C(-1,0).