题目内容
6. 方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).(1)作出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标;
(2)作出△ABC绕点O逆时针旋转90°后得到的△A2B2C2,并求出C2所经过的路径长.
分析 (1)分别作出各点关于y轴的对称点,再顺次连接即可,根据点在坐标系中的位置写出点坐标即可;
(2)分别作出各点绕点O逆时针旋转90°后得到的对称点,再顺次连接即可,根据弧长公式计算可得C2所经过的路径长.
解答 解:(1)如图,△A1B1C1即为所求作三角形A1(-5,-4);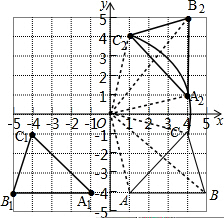
(2)如图,△A2B2C2即为所求作三角形,
∵OC2=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
∴C2所经过的路径$\widehat{C{C}_{2}}$的长为$\frac{90•π•\sqrt{17}}{180}$=$\frac{\sqrt{17}}{2}$π.
点评 本题考查的是作图-轴对称变换、旋转变换,作出各顶点轴对称变换和旋转变换的对应点是解答此题作图的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
14.下列各组数是三角形的三边,能组成直角三角形的一组数是( )
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 2,3,4 | C. | 3,4,5 | D. | 6,8,12 |
18.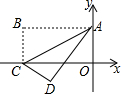 如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
 如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )| A. | (-$\frac{12}{5}$,-$\frac{6}{5}$) | B. | (-$\frac{12}{5}$,-$\frac{8}{5}$) | C. | ($\frac{12}{5}$,-$\frac{6}{5}$) | D. | ($\frac{12}{5}$,-$\frac{8}{5}$) |
16.下列命题中的真命题是( )
| A. | 有一组对边平行的四边形是平行四边形 | |
| B. | 有一个角是直角的四边形是矩形 | |
| C. | 顺次连结矩形各中点所得的四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
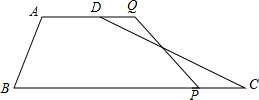 如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q.
如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q. 如图,△ABC的三个顶点分别为A(1,1)、B(4,2)、C(3,4).
如图,△ABC的三个顶点分别为A(1,1)、B(4,2)、C(3,4). 如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.
如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.