题目内容
10.答下列各题:(1)若x+y=3,xy=2,求x2+y2的值;
(2)若x-y=1,x2+y2=25,求x3y-2x2y2+xy3的值.
分析 (1)把x2+y2变为(x+y)2-2xy,整体代入求得答案即可;
(2)由x-y=1,x2+y2=25求得xy,进一步把代数式x3y-2x2y2+xy3先利用提取公因式法,再利用完全平方公式因式分解,整体代入求得数值即可.
解答 解:(1)x2+y2=(x+y)2-2xy=32-2×2=5;
(2)x3y-2x2y2+xy3=xy(x2-2xy+y2)=xy(x-y)2;
∵x-y=1,
∴(x-y)2=1,
∴x2+y2-2xy=1,
又∵x2+y2=25,
∴xy=12,
∴x3y-2 x2 y2+xy3=xy(x-y)2=12.
点评 此题考查因式分解的实际运用,掌握完全平方公式,利用整体代入的方法是解决问题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
18.若2x+3y=3,则4x•8y=( )
| A. | 8 | B. | 6 | C. | 9 | D. | 90° |
15. 如图所示,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( )
如图所示,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( )
 如图所示,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( )
如图所示,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( )| A. | 24cm2 | B. | 18cm2 | C. | 12cm2 | D. | 30cm2 |
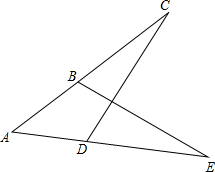 如图,AD=AB,∠C=∠E,AB=3,AE=8.则DE=5.
如图,AD=AB,∠C=∠E,AB=3,AE=8.则DE=5.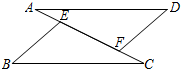 如图所示,已知AE=CF,∠A=∠C,要使△BCE≌△DAF,还需添加一个条件(只需填一个即可)AD=BC或∠B=∠D或∠CEB=∠AFD.
如图所示,已知AE=CF,∠A=∠C,要使△BCE≌△DAF,还需添加一个条件(只需填一个即可)AD=BC或∠B=∠D或∠CEB=∠AFD.