题目内容
19.已知二次函数y=x2-4x+8,当-4≤x≤1时,函数y的取值范围为5≤y≤40.分析 先根据a=1判断出抛物线的开口向上,故有最小值,再把抛物线化为顶点式的形式可知对称轴x=2,再根据-4≤x≤1,可知当x=-4时y最大,把x=1时y最小代入即可得出结论.
解答 解:∵a=1,
∴抛物线的开口向上,故有最小值,
∵对称轴x=2,根据-4≤x≤1,
∴y随x的增大而减小,
∴当x=-4时y最大为40,
当x=1时y最小为5,
∴函数y的取值范围为5≤y≤40,
故答案为5≤y≤40.
点评 本题考查了二次函数的性质,掌握抛物线的开口方向、对称轴以及增减性是解题的关键.

练习册系列答案
相关题目
7.下列各组数中,相等的一组是( )
| A. | -24与(-2)4 | B. | 53与3 | C. | -(-3)与-|-3| | D. | (-1)3与(-1)2013 |
 已知:AD是ABC的边BC上的高,AE是△ABC的外接圆的直径.
已知:AD是ABC的边BC上的高,AE是△ABC的外接圆的直径.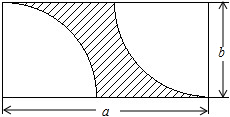 嘉鱼县为创建国家卫生城市,要在人民广场修建一个长方形花坛,面向全县人民征集设计方案,我校同学积极参与.如图所示是七(9)班龚克同学设计的得意之作:
嘉鱼县为创建国家卫生城市,要在人民广场修建一个长方形花坛,面向全县人民征集设计方案,我校同学积极参与.如图所示是七(9)班龚克同学设计的得意之作: