题目内容
20.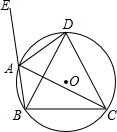 如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.
如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.求证:DB=DC.
分析 先根据圆周角定理得出∠DAC=∠DBC,再由角平分线的性质得出∠EAD=∠DAC,根据圆内接四边形的性质得出∠EAD=∠BCD,由此可得出结论.
解答 证明:∵∠DAC与∠DBC是同弧所对的圆周角,
∴∠DAC=∠DBC.
∵AD平分∠CAE,
∴∠EAD=∠DAC,
∴∠EAD=∠DBC.
∵四边形ABCD内接于⊙O,
∴∠EAD=∠BCD,
∴∠DBC=∠DCB,
∴DB=DC.
点评 本题考查的是圆内接四边形的性质,熟知圆内接四边形的任意一个外角等于它的内对角是解答此题的关键.

练习册系列答案
相关题目
8.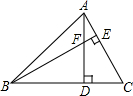 如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
 如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
12.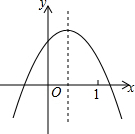 已知二次函数y=ax2+bx+c的图象如图所示,则下列选项中不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列选项中不正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则下列选项中不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列选项中不正确的是( )| A. | a<0 | B. | c>0 | C. | 0<-$\frac{b}{2a}$<1 | D. | a+b+c<0 |
 如图,AB为⊙O直径,点C,D在⊙O上,若∠DCB=30°,则∠DBA=60°.
如图,AB为⊙O直径,点C,D在⊙O上,若∠DCB=30°,则∠DBA=60°.
 画出如图所示几何体的三视图.
画出如图所示几何体的三视图.