题目内容
11.已知,△ABE内接于⊙O,BC为⊙O的切线.(1)如图1,求证:∠BAE=∠CBE;
(2)如图2,连接AC交BE于点D,交⊙O于点L,若∠C+∠E=180°,求证:AB=AC;
(3)在(2)的条件下,∠ABE=2∠CAE,BD=5,AB=7,求DL的长.
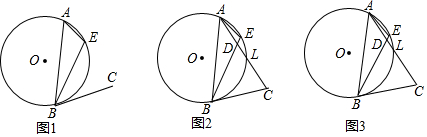
分析 (1)过点B作直径BF,连接EF,如图1,利用切线的性质得∠FBE+∠CBE=90°,再根据圆周角定理得到∠BEF=90°,∠BAE=∠F,于是可得到∠BAE=∠CBE;
(2)连接BL,如图2,根据圆周角定理得到∠E=∠ALB,利用等角的补角相等得到∠BLC=∠C,再利用(1)的结论得∠CBL=∠CAB,所以∠BLC=∠ABC=∠C,则根据等腰三角形的判定定理得到AB=AC;
(3)作BH⊥CD于H,连接BL,如图3,设∠CAE=x,∠C=y,则∠ABE=2x,∠E=180°-y,利用∠DAE+∠E=∠CBD+∠BCD可得到y=x+60°,则∠C=x+60°,∠CBD=60°-x,利用三角形内角和定理可计算出∠BDC=60°,根据含30度的直角三角形三边的关系得到DH=$\frac{1}{2}$BD=$\frac{5}{2}$,BH=$\sqrt{3}$DH=$\frac{5\sqrt{3}}{2}$,接着根据勾股定理可计算出AH=$\frac{11}{2}$,则CH=$\frac{3}{2}$,然后根据等腰三角形的性质得CH=LH=$\frac{3}{2}$,最后计算DH-LH即可.
解答 (1)证明:过点B作直径BF,连接EF,如图1,
∵BC为⊙O的切线,
∴FB⊥BC,
∴∠FBE+∠CBE=90°,
∵BF为直径,
∴∠BEF=90°,
∴∠F+∠FBE=90°,
∴∠F=∠CBE,
∵∠BAE=∠F,
∴∠BAE=∠CBE;
(2)证明:连接BL,如图2,
∵∠E=∠ALB,
而∠ALB+∠BLC=180°,∠C+∠E=180°,
∴∠BLC=∠C,
由(1)得∠CBL=∠CAB,
∴∠BLC=∠ABC=∠C,
∴AB=AC;
(3)解:作BH⊥CD于H,连接BL,如图3,
设∠CAE=x,∠C=y,则∠ABE=2x,∠E=180°-y,
∵∠ABC=∠C=y,
∴∠CBE=y-2x,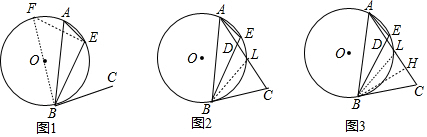
∵∠DAE+∠E=∠CBD+∠BCD,
即x+180°-y=y-2x+y,
∴y=x+60°,
即∠C=x+60°,∠CBD=60°-x,
∴∠BDC=180°-(x+60°+60°-x)=60°,
在Rt△BDH中,DH=$\frac{1}{2}$BD=$\frac{5}{2}$,BH=$\sqrt{3}$DH=$\frac{5\sqrt{3}}{2}$,
在Rt△ABH中,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\sqrt{{7}^{2}-(\frac{5\sqrt{3}}{2})^{2}}$=$\frac{11}{2}$,
∵AC=AB=7,
∴CH=7-$\frac{11}{2}$=$\frac{3}{2}$,
∵∠BLC=∠C,BH⊥CL,
∴CH=LH=$\frac{3}{2}$,
∴DL=DH-LH=$\frac{5}{2}$-$\frac{3}{2}$=1.
点评 本题考查了圆的综合题:熟练掌握等腰三角形的性质、圆周角定理和切线的性质,会应用勾股定理和含30度的直角三角形三边的关系计算线段的长;理解(1)小题的结论解决(2)小题.

 阅读快车系列答案
阅读快车系列答案| A. | 2a-1≥0 | B. | 2a+1≥0 | C. | 2a-1<0 | D. | 2a+1<0 |
| A. | 5,$\sqrt{10}$ | B. | -5,$\sqrt{10}$ | C. | 5,±$\sqrt{10}$ | D. | -5,±$\sqrt{10}$ |
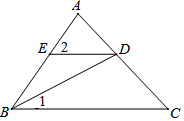 已知,如图,BD平分∠ABC,∠1=25°,∠2=50°.试判断ED与BC的位置关系并说明理由.
已知,如图,BD平分∠ABC,∠1=25°,∠2=50°.试判断ED与BC的位置关系并说明理由.