题目内容
1.在平面直角坐标系中画出两条相交直线y=x和y=kx+b,交点为(x0,y0),在x轴上表示出不与x0重合的x1,先在直线y=kx+b上确定点(x1,y1),再在直线y=x上确定纵坐标为y1的点(x2,y1),然后在x轴上确定对应的数x2,…,依此类推到(xn,yn-1),我们来研究随着n的不断增加,xn的变化情况.如图1,若k=2,b=-4,随着n的不断增加,xn逐渐远离(填“靠近”或“远离”)x0;如图2,若k=-$\frac{2}{3}$,b=2,随着n的不断增加,xn逐渐靠近(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0,则k的取值范围为k<0.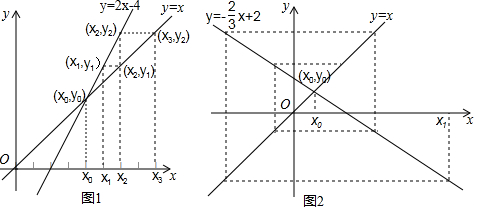
分析 观察图1以及图2中,点(xn,yn-1)的位置即可解决问题.
解答 解:如图1,若k=2,b=-4,随着n的不断增加,xn逐渐远离x0,
如图2,若k=-$\frac{2}{3}$,b=2,随着n的不断增加,xn逐渐靠近x0,
由此可知,若随着n的不断增加,xn逐渐靠近x0,则k的取值范围为k<0.
故答案为远离,靠近、k<0;
点评 本题考查一次函数与系数的关系、规律型-点的坐标等知识,解题的关键是理解题意,学会读懂图象信息解决问题,属于中考创新题目.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
2.已知3cm,4cm和45°画三角形,画出的不同三角形的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
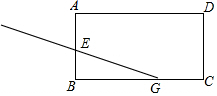 如图,在矩形ABCD中,BG=10,BC=13,将纸片沿过点G的折痕GE折叠,使顶点B的对称点F落在边AD上,折痕与矩形的边交于点E,若满足条件的F点有2个时,AB的取值范围$\sqrt{91}$≤AB<10..
如图,在矩形ABCD中,BG=10,BC=13,将纸片沿过点G的折痕GE折叠,使顶点B的对称点F落在边AD上,折痕与矩形的边交于点E,若满足条件的F点有2个时,AB的取值范围$\sqrt{91}$≤AB<10..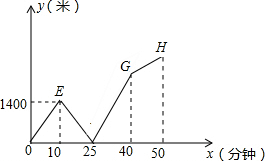 如图,小明和小亮同时从学校放学,两人以各自速度匀速步行回家,小明的家在学校的正西方向,小亮的家在学校的正东方向,小明准备一回家就开始做作业,打开书包时发现错拿了小亮的练习册,于是立即跑步去追小亮,终于在途中追上了小亮并交还了练习册,然后再以先前的速度步行回家,(小明在家中耽搁和交还作业的时间忽略不计)结果小明比小亮晚回到家中.如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图.则小明的家和小亮的家相距2975米.
如图,小明和小亮同时从学校放学,两人以各自速度匀速步行回家,小明的家在学校的正西方向,小亮的家在学校的正东方向,小明准备一回家就开始做作业,打开书包时发现错拿了小亮的练习册,于是立即跑步去追小亮,终于在途中追上了小亮并交还了练习册,然后再以先前的速度步行回家,(小明在家中耽搁和交还作业的时间忽略不计)结果小明比小亮晚回到家中.如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图.则小明的家和小亮的家相距2975米.