题目内容
12.如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上),现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示,根据图象提供下列4个信息: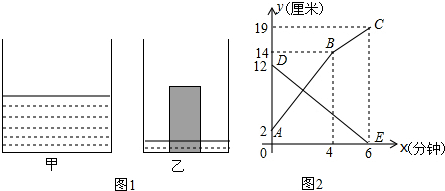
①注水2分钟时,甲、乙两个水槽中水的深度相同;
②乙槽中铁块的高度为12厘米;
③若乙槽底面积为36平方厘米(壁厚不计),乙槽中铁块体积为72立方厘米;
④若乙槽中铁块的体积为112立方厘米,甲槽底面积为60平方厘米.正确的有( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①观察函数图象找出点的坐标,利用待定系数法求出两函数的关系式,令y甲=y乙求出x值,即可得出信息①正确;②根据点B的纵坐标,即可得出乙槽中铁块的高度为14厘米,信息②不正确;③先求出若乙槽中没有铁块,乙槽水位上升高度,根据多升高的水的体积为铁块体积的$\frac{14}{12}$,即可求出乙槽中铁块体积,信息③不正确;④结合③多升高的水的体积为铁块体积的$\frac{14}{12}$,可求出甲槽中水的总体积,除以高度即可得出甲槽底面积,信息④正确.综上即可得出结论.
解答 解:①利用待定系数法可求出y甲=-2x+12(0≤x≤6),y乙=$\left\{\begin{array}{l}{3x+2(0≤x≤4)}\\{\frac{5}{2}x+4(4≤x≤6)}\end{array}\right.$,
令-2x+12=3x+2,解得:x=2,
∴注水2分钟时,甲、乙两个水槽中水的深度相同,信息①正确;
②∵点B(4,14)为转折点,
∴乙槽中铁块的高度为14厘米,信息②不正确;
③若乙槽中没有铁块,则乙槽水位上升高度为(19-14)×$\frac{6}{6-4}$=15(厘米),
∴乙槽中铁块体积为(19-2-15)×36×$\frac{14}{14-2}$=84(立方厘米),信息③不正确;
④结合③可知:甲槽底面积为112×$\frac{14-2}{14}$×$\frac{15}{19-2-15}$÷12=60(平方厘米),信息④正确.
综上所述:正确的结论有①④.
故选B.
点评 本题考查了函数的图象、待定系数法求一次函数解析式以及体积,逐一分析四条信息的正误是解题的关键.

练习册系列答案
相关题目
2.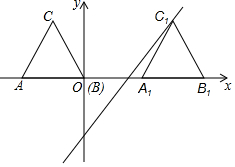 如图,等腰三角形ABC的底边AB在x轴上,点B与原点O重合,已知点A(-2,0),AC=$\sqrt{5}$,将△ABC沿x轴向右平移,当点C的对应点C1落在直线y=2x-4上时,则平移的距离是( )
如图,等腰三角形ABC的底边AB在x轴上,点B与原点O重合,已知点A(-2,0),AC=$\sqrt{5}$,将△ABC沿x轴向右平移,当点C的对应点C1落在直线y=2x-4上时,则平移的距离是( )
 如图,等腰三角形ABC的底边AB在x轴上,点B与原点O重合,已知点A(-2,0),AC=$\sqrt{5}$,将△ABC沿x轴向右平移,当点C的对应点C1落在直线y=2x-4上时,则平移的距离是( )
如图,等腰三角形ABC的底边AB在x轴上,点B与原点O重合,已知点A(-2,0),AC=$\sqrt{5}$,将△ABC沿x轴向右平移,当点C的对应点C1落在直线y=2x-4上时,则平移的距离是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20.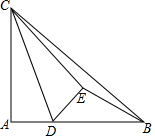 如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB上一动点,将△ACD沿CD翻折得到△ECD,那么BE的最小值为( )
如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB上一动点,将△ACD沿CD翻折得到△ECD,那么BE的最小值为( )
 如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB上一动点,将△ACD沿CD翻折得到△ECD,那么BE的最小值为( )
如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB上一动点,将△ACD沿CD翻折得到△ECD,那么BE的最小值为( )| A. | $\sqrt{3}$ | B. | 4-$\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
7.一个底面直径为2,高为3的圆锥的体积是( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
4.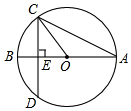 如图,在⊙O中,弦CD垂直直径AB于点E,已知OC=4,CD=4$\sqrt{2}$,则∠BAC的度数为( )
如图,在⊙O中,弦CD垂直直径AB于点E,已知OC=4,CD=4$\sqrt{2}$,则∠BAC的度数为( )
 如图,在⊙O中,弦CD垂直直径AB于点E,已知OC=4,CD=4$\sqrt{2}$,则∠BAC的度数为( )
如图,在⊙O中,弦CD垂直直径AB于点E,已知OC=4,CD=4$\sqrt{2}$,则∠BAC的度数为( )| A. | 15° | B. | 22.5° | C. | 30° | D. | 45° |
 如图,在△ABC中,点D,E分别是边AB,AC上的点,且DE∥BC,若$\frac{AD}{DB}=\frac{1}{2}$,DE=3,则BC的长度是( )
如图,在△ABC中,点D,E分别是边AB,AC上的点,且DE∥BC,若$\frac{AD}{DB}=\frac{1}{2}$,DE=3,则BC的长度是( )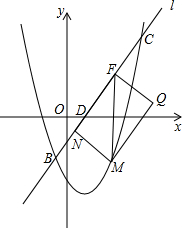 已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).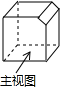 如图,是一个正方体被切掉一条棱后所得的几何体,则它的左视图是( )
如图,是一个正方体被切掉一条棱后所得的几何体,则它的左视图是( )