题目内容
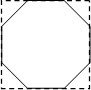 如图,正方形的边长为
如图,正方形的边长为| 2 |
考点:正方形的性质,正多边形和圆
专题:
分析:设剪去三角形的直角边长x,根据勾股定理可得,三角形的斜边长为
x,即正八边形的边长为
x,依题意得
x+2x=
+2,解方程即可求出正八边形的边.用正方形的面积减去4个等腰直角三角形的面积即可求得正八边形的面积.
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:设剪去三角形的直角边长x,根据勾股定理可得,三角形的斜边长为
x,即正八边形的边长为
x,
∴
x+2x=
+2,
∴x=1,
∴正八边形的边长等于
x=
,
∴正八边形的面积=(
+2)2-4×
×12=4+4
.
| 2 |
| 2 |
∴
| 2 |
| 2 |
∴x=1,
∴正八边形的边长等于
| 2 |
| 2 |
∴正八边形的面积=(
| 2 |
| 1 |
| 2 |
| 2 |
点评:本题考查了正方形和正八边形的性质以及勾股定理的运用,解题的关键是设出未知数用列方程的方法解决几何问题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
下列判断中正确的是( )
| A、四边相等的四边形是正方形 |
| B、四角相等的四边形是矩形 |
| C、对角线互相垂直的平行四边形是正方形 |
| D、对角线互相垂直的四边形是菱形 |
在函数y=kx(k<0)的图象上有A(1,y1),B(-1,y2),C(-2,y3)三个点,则下列各式正确的是( )
| A、y1<y2<y3 |
| B、y1<y3<y2 |
| C、y3<y2<y1 |
| D、y2<y3<y1 |
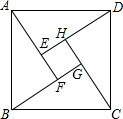 四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图.它是由四个相同的直角三角形(Rt△AED,Rt△BFA,Rt△CGB,Rt△DHC)与中间的小正方形EFGH拼成的,
四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图.它是由四个相同的直角三角形(Rt△AED,Rt△BFA,Rt△CGB,Rt△DHC)与中间的小正方形EFGH拼成的, 如图,AC平分∠BAD,CE⊥AB于E,BC=CD,∠ADC+∠B=180°,探究2AE与AB,AD的数量关系,并加以证明.
如图,AC平分∠BAD,CE⊥AB于E,BC=CD,∠ADC+∠B=180°,探究2AE与AB,AD的数量关系,并加以证明.