题目内容
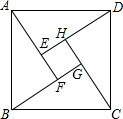 四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图.它是由四个相同的直角三角形(Rt△AED,Rt△BFA,Rt△CGB,Rt△DHC)与中间的小正方形EFGH拼成的,
四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图.它是由四个相同的直角三角形(Rt△AED,Rt△BFA,Rt△CGB,Rt△DHC)与中间的小正方形EFGH拼成的,(1)试说明拼成的四边形ABCD是正方形.
(2)若四边形ABCD的面积为13.每个直角三角形两直角边的和为5,求中间小正方形EFGH的面积.
考点:正方形的性质
专题:
分析:(1)根据Rt△AED≌Rt△BFA≌Rt△CGB≌Rt△DHC,即可证得四边形ABCD是正方形;
(2)设直角三角形的直角边中长边为a,短边为b,根据大正方形面积为13和a+b=5列出方程组,解方程组即可解题.
(2)设直角三角形的直角边中长边为a,短边为b,根据大正方形面积为13和a+b=5列出方程组,解方程组即可解题.
解答:解:(1)∵Rt△AED≌Rt△BFA≌Rt△CGB≌Rt△DHC,
∴AB=BC=CD=DA,∠BAF=∠ADE=∠DCH=∠CBG,∠ABF=∠DAE=∠CDH=∠BCG,
∵∠BAF+∠ABF=∠ADE+∠DAE=∠DCH+∠CDH=∠CBG+∠BCG=90°,
∴∠BAF+∠DAE=∠ADE+∠CDH=∠DCH+∠BCG=∠CBG+∠ABF=90°,
∴∠BAD=∠ADC=∠DCB=∠CBA=90°,
∴四边形ABCD是正方形;
(2)设直角三角形的长直角边为a,短直角边为b,
则存在
,
解得
.
则小正方形EFGH的面积为(3-2)2=1.
答:小正方形的EFGH面积为1.
∴AB=BC=CD=DA,∠BAF=∠ADE=∠DCH=∠CBG,∠ABF=∠DAE=∠CDH=∠BCG,
∵∠BAF+∠ABF=∠ADE+∠DAE=∠DCH+∠CDH=∠CBG+∠BCG=90°,
∴∠BAF+∠DAE=∠ADE+∠CDH=∠DCH+∠BCG=∠CBG+∠ABF=90°,
∴∠BAD=∠ADC=∠DCB=∠CBA=90°,
∴四边形ABCD是正方形;
(2)设直角三角形的长直角边为a,短直角边为b,
则存在
|
解得
|
则小正方形EFGH的面积为(3-2)2=1.
答:小正方形的EFGH面积为1.
点评:本题考查了正方形的判定和性质,勾股定理在直角三角形中的灵活应用,正确列出方程组并且求解是解题的关键.

练习册系列答案
相关题目
 如图,已知BD=CE=AF,△ABC是正三角形,证明:△DEF是正三角形.
如图,已知BD=CE=AF,△ABC是正三角形,证明:△DEF是正三角形.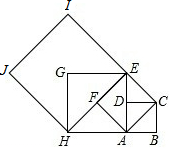 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2=
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2= 如图,正方形的边长为
如图,正方形的边长为