题目内容
已知二次函数y=x2-mx+m-2:
(1)求证:不论m为任何实数,此二次函数的图象与x轴都有两个交点;
(2)当二次函数的图象经过点(3,6)时,确定m的值,并写出此二次函数与坐标轴的交点坐标..
(1)求证:不论m为任何实数,此二次函数的图象与x轴都有两个交点;
(2)当二次函数的图象经过点(3,6)时,确定m的值,并写出此二次函数与坐标轴的交点坐标..
考点:抛物线与x轴的交点
专题:
分析:(1)先计算判别式得到△=(m-2)2+4,再根据非负数的性质得△>0,然后根据抛物线与x轴的交点问题即可得到结论.
(2)把点(3,6)代入函数解析式中即可求出m的值,也可以求出二次函数的解析式.
(2)把点(3,6)代入函数解析式中即可求出m的值,也可以求出二次函数的解析式.
解答:(1)证明:△=m2-4(m-2)=(m-2)2+4,
∵(m-2)2≥0,
∴(m-2)2+4>0,即△>0,
∴无论m取何实数,抛物线总与x轴有两个交点.
(2)解:∵二次函数的图象经过点(3,6),
∴6=9-3m+m-2,
∴m=
,
∴y=x2-
x-
.
当x=0时,y=-
,即该函数图象与y轴交于点(0,-
).
当y=0时,x2-
x-
=2(x+1)(2x-3)=0,
解得 x1=-1,x2=
.
则该函数图象与x轴的交点坐标是:(-1,0)、(
,0).
综上所述,m的值是
,该函数图象与y轴交于点(0,-
),与x轴的交点坐标是:(-1,0)、(
,0).
∵(m-2)2≥0,
∴(m-2)2+4>0,即△>0,
∴无论m取何实数,抛物线总与x轴有两个交点.
(2)解:∵二次函数的图象经过点(3,6),
∴6=9-3m+m-2,
∴m=
| 1 |
| 2 |
∴y=x2-
| 1 |
| 2 |
| 3 |
| 2 |
当x=0时,y=-
| 3 |
| 2 |
| 3 |
| 2 |
当y=0时,x2-
| 1 |
| 2 |
| 3 |
| 2 |
解得 x1=-1,x2=
| 3 |
| 2 |
则该函数图象与x轴的交点坐标是:(-1,0)、(
| 3 |
| 2 |
综上所述,m的值是
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点与一元二次方程ax2+bx+c=0根之间的关系:△=b2-4ac决定抛物线与x轴的交点个数;△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
如图中是轴对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,已知BD=CE=AF,△ABC是正三角形,证明:△DEF是正三角形.
如图,已知BD=CE=AF,△ABC是正三角形,证明:△DEF是正三角形.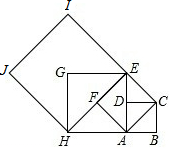 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2=
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2= 有一抛物线型的渡槽,当水位在AB位置时,水的最大深度为2米,水面宽4米,当水面上升1米时,水面宽多少米?
有一抛物线型的渡槽,当水位在AB位置时,水的最大深度为2米,水面宽4米,当水面上升1米时,水面宽多少米?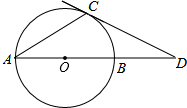 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.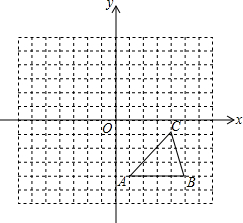 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1). 如图,正方形的边长为
如图,正方形的边长为 如图,圆O的一条弦AB将圆周长分为3:7两部分,试求弦AB所对的圆心角和圆周角的度数,并作出图.
如图,圆O的一条弦AB将圆周长分为3:7两部分,试求弦AB所对的圆心角和圆周角的度数,并作出图.