题目内容
某服装厂现有A种布料35m,B种布料26m,现计划用这两种布料生产男、女两种款式的时装共40套.已知做一套男时装需要A种布料0.6m,B种布料0.9m,可获利90元;做一套女时装需要A种布料1.1m,B种布料0.4m,可获利100元.若设生产男时装套数为x套,用这批布料生产这两种时装所获的总利润为y元.
(1)求y与x的函数关系式,并求出x的取值范围;
(2)该服装厂在生产这批时装中,当生产男时装多少套时,所获利润最大?最大利润是多少元?
(1)求y与x的函数关系式,并求出x的取值范围;
(2)该服装厂在生产这批时装中,当生产男时装多少套时,所获利润最大?最大利润是多少元?
考点:一次函数的应用
专题:
分析:(1)由于计划用这两种布料生产男、女两种款式的时装共40套,设生产男时装套数为x套,用这批布料生产两种时装所获得的总利润为y元,做一套男时装可获利90元;做女时装 可获利100元,由此即可求解;
(2)进一步根据一次函数的增减性求出所获利润最大值即可.
(2)进一步根据一次函数的增减性求出所获利润最大值即可.
解答:解:(1)设生产男时装的套数为x,则生产女时装为(40-x),由题意,得
y=90x+100(40-x)=-10x+4000;
由题意得
,
解得不等式组的解集是18≤x≤20;
(2)∵x为整数,
∴x=18,19,20,
∴y与x的函数关系式是y=-10x+4000(x=18,19,20);
∵k=-10<0,
∴y随x的增大而减小,
∴当x=18时,y最大=3820,
即生产男时装18套时,该厂所获利润最大,最大利润是3820元.
y=90x+100(40-x)=-10x+4000;
由题意得
|
解得不等式组的解集是18≤x≤20;
(2)∵x为整数,
∴x=18,19,20,
∴y与x的函数关系式是y=-10x+4000(x=18,19,20);
∵k=-10<0,
∴y随x的增大而减小,
∴当x=18时,y最大=3820,
即生产男时装18套时,该厂所获利润最大,最大利润是3820元.
点评:本题考查了一次函数的应用,一元一次不等式组的应用,利用一次函数求最值时,关键是应用一次函数的性质:即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
相关题目
具备下列条件的两个三角形中,不一定全等的是( )
| A、有两边一角对应相等 |
| B、三边对应相等 |
| C、两角一边对应相等 |
| D、有两边对应相等的两个直角三角形 |
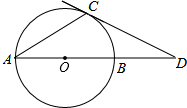 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.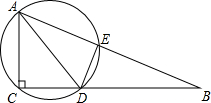 如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.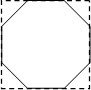 如图,正方形的边长为
如图,正方形的边长为