题目内容
19.已知关于x的一元二次方程x2+2ax+b2=0,a>0,b>0.(1)若方程有实数根,试确定a,b之间的大小关系;
(2)若a:b=2:$\sqrt{3}$,且2x1-x2=2,求a,b的值.
分析 (1)根据方程有实数根,得出判别式△≥0,再根据a>0,b>0,即可得出答案;
(2)利用a与b的比值分别设出a和b,利用根与系数的关系用设出的未知数表示出方程的两个解,代入的2x1-x2=2中求得a与b的值即可.
解答 解:(1)∵方程x2+2ax+b2=0有实数根,
∴△=(2a)2-4b2≥0,即a2≥b2,
∵a>0,b>0,
∴a≥b;
(2)∵a:b=2:$\sqrt{3}$,
∴设a=2k,b=$\sqrt{3}$k.
解关于x的一元二次方程x2+4kx+3k2=0,得x=-k或-3k,
当x1=-k,x2=-3k时,由2x1-x2=2得k=2,
当x1=-3k,x2=-k时,由2x1-x2=2得k=-$\frac{2}{5}$(不合题意,舍去),
∴a=4,b=2$\sqrt{3}$.
点评 本题主要考查了根的判别式的知识,解答本题要掌握一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
10.已知$\frac{x-y}{x+y}=3$,则代数式$\frac{x-y}{x+y}+$$\frac{3(x+y)}{x-y}+$$\frac{7}{2}$的值为( )
| A. | 8 | B. | 7 | C. | $\frac{15}{2}$ | D. | 6 |
7.直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),则不等式x2+bx+c>x+m的解集为( )
| A. | 0<x<2 | B. | x<2 | C. | 0<x<3 | D. | x<1或x>3 |
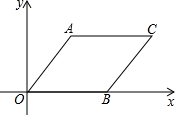 如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则菱形的周长为20,点B的坐标是(5,0).
如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则菱形的周长为20,点B的坐标是(5,0).