题目内容
3.计算:(1)$\frac{c}{a{b}^{2}}$$+\frac{bc}{a{b}^{2}}$;
(2)$\frac{3}{a}+\frac{a-15}{5a}$;
(3)$\frac{1}{{R}_{1}}$$+\frac{1}{{R}_{2}}$;
(4)$\frac{b}{a+b}$$+\frac{ab}{{b}^{2}-{a}^{2}}$.
分析 (1)根据同分母分式的加法进行计算即可;
(2)对原分式先通分,再相加即可;
(3)对原分式先通分再相加即可;
(4)对原分式先通分再相加即可.
解答 解:(1)$\frac{c}{a{b}^{2}}$$+\frac{bc}{a{b}^{2}}$
=$\frac{c+bc}{a{b}^{2}}$;
(2)$\frac{3}{a}+\frac{a-15}{5a}$
=$\frac{3×5+(a-15)}{5a}$
=$\frac{15+a-15}{5a}$
=$\frac{a}{5a}$
=$\frac{1}{5}$;
(3)$\frac{1}{{R}_{1}}$$+\frac{1}{{R}_{2}}$
=$\frac{{R}_{2}+{R}_{1}}{{R}_{1}{R}_{2}}$;
(4)$\frac{b}{a+b}$$+\frac{ab}{{b}^{2}-{a}^{2}}$
=$\frac{b(b-a)+ab}{(b+a)(b-a)}$
=$\frac{{b}^{2}-ab+ab}{(b+a)(b-a)}$
=$\frac{{b}^{2}}{{b}^{2}-{a}^{2}}$.
点评 本题考查分式的加减法,解题的关键是明确分式加减法的计算方法.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
11.解不等式组$\left\{\begin{array}{l}{2(2x-1)+1≤3x}\\{\frac{3x+1}{2}>x-1}\end{array}\right.$并将解集在数轴上表示出来.
18.函数y=2x2+1有( )
| A. | 最大值1 | B. | 最小值1 | C. | 最大值0 | D. | 最小值0 |
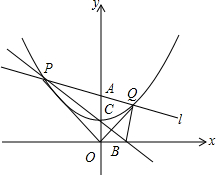 如图,在直角坐标系中,直线l是绕着定点A(0,2)旋转的动直线,且与经过点C(0,1)的抛物线y=$\frac{1}{4}{x}^{2}+h$交于不同的两点P和Q(即直线l在旋转过程中,不与y轴平行).
如图,在直角坐标系中,直线l是绕着定点A(0,2)旋转的动直线,且与经过点C(0,1)的抛物线y=$\frac{1}{4}{x}^{2}+h$交于不同的两点P和Q(即直线l在旋转过程中,不与y轴平行).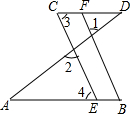 如图,∠3=∠B,∠1=∠2,求证:CD∥AB.
如图,∠3=∠B,∠1=∠2,求证:CD∥AB.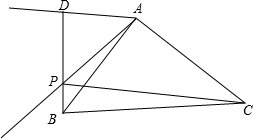 在△ABC中,∠BAC=90°,作∠DAP=∠ABC=45°,过点B作BD⊥AD,垂足为D,BD交直线AP于P.
在△ABC中,∠BAC=90°,作∠DAP=∠ABC=45°,过点B作BD⊥AD,垂足为D,BD交直线AP于P.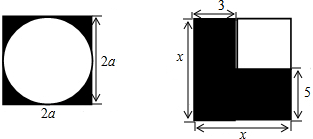 求各图中的阴影面积(单位:cm)
求各图中的阴影面积(单位:cm)