Question

8．如图，在等腰△ABC中，AC=BC=5cm，AB=6cm，求△ABC的面积．

Answer 1

分析 过点C作CD⊥AB于点D，根据等腰三角形的性质即可得出AD=BD=$\frac{1}{2}$AB=3cm，在Rt△ADC中，利用勾股定理即可求出CD的长度，再根据三角形的面积公式即可得出结论．

解答 解：过点C作CD⊥AB于点D，如图所示．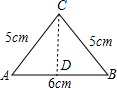
∵AC=BC=5cm，AB=6cm，
∴AD=BD=$\frac{1}{2}$AB=3cm．
∵CD⊥AB，
∴∠ADC=90°，
在Rt△ADC中，AC=5cm，AD=3cm，
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=4cm．
∴S_△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×6×4=12cm²．

点评 本题考查了勾股定理以及等腰三角形的性质，解题的关键求出CD的长度．本题属于基础题，难度不大，解决该题型题目时，根据勾股定理求出等腰三角形的高的长度是关键．