题目内容
13.先将一矩形ABCD置于直角坐标系中(AB=4,BC=3),使点A与坐标系中原点重合,边AB、AD分别落在x轴、y轴上(如图1),再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图2),则图2中点C的坐标为($\frac{4\sqrt{3}-3}{2}$,$\frac{3\sqrt{3}+4}{2}$).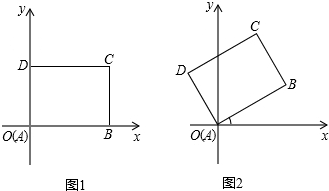
分析 根据旋转的性质,首先得出OM,DM的长,进而求出ON,NC的长即可得出答案.
解答 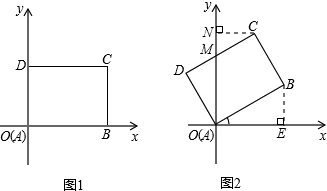 解:∵AB=4,BC=3,
解:∵AB=4,BC=3,
∴图1中点C的坐标为(4,3),
在图2中,设CD与y轴交于点M,作CN⊥y轴于点N,那么∠DOM=30°,OD=3,
∴DM=3•tan30°=$\sqrt{3}$,OM=3÷cos30°=2$\sqrt{3}$,
那么CM=4-$\sqrt{3}$,易知∠NCM=30°,
∴MN=CM•sin30°=$\frac{4-\sqrt{3}}{2}$,CN=CM•cos30°=$\frac{4\sqrt{3}-3}{2}$,
则ON=OM+MN=$\frac{3\sqrt{3}+4}{2}$,
∴图2中C点的坐标为:($\frac{4\sqrt{3}-3}{2}$,$\frac{3\sqrt{3}+4}{2}$).
故答案为:($\frac{4\sqrt{3}-3}{2}$,$\frac{3\sqrt{3}+4}{2}$).
点评 此题考查了矩形的性质以及旋转问题,关键是根据旋转前后对应角的度数不变,对应线段的长度不变,注意构造直角三角形求解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
5.已知:x-2y=-3,则代数式(2y-x)2-2x+4y-1的值为( )
| A. | 2 | B. | 14 | C. | -4 | D. | 0 |
 如图,在△ABC中,BP、AP是∠ABC、∠BAC的角平分线,交点为P,PD⊥BC于D,PE⊥AC于E,PD=4.则PE=4.
如图,在△ABC中,BP、AP是∠ABC、∠BAC的角平分线,交点为P,PD⊥BC于D,PE⊥AC于E,PD=4.则PE=4.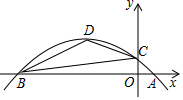 二次函数y=ax2+bx+c 的图象与x轴交于A(1,0),B两点,与y轴交于点C,其顶点D的坐标为(-3,2).
二次函数y=ax2+bx+c 的图象与x轴交于A(1,0),B两点,与y轴交于点C,其顶点D的坐标为(-3,2).