题目内容
18.甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
分析 (1)根据题意可以列出相应的分式方程,从而可以求得甲的平均攀登速度;
(2)根据(1)中甲的速度可以表示出丙的速度,再用甲的速度比丙的平均攀登速度即可解答本题.
解答 解:(1)设乙的速度为x米/分钟,
$\frac{900}{1.2x}+15=\frac{900}{x}$,
解得,x=10,
经检验,x=10是原分式方程的解,
∴1.2x=12,
即甲的平均攀登速度是12米/分钟;
(2)设丙的平均攀登速度是y米/分,
$\frac{h}{12}+0.5×60=\frac{h}{y}$,
化简,得
y=$\frac{12h}{h+360}$,
∴甲的平均攀登速度是丙的:$\frac{12}{\frac{12h}{h+360}}=\frac{h+360}{h}$倍,
即甲的平均攀登速度是丙的$\frac{h+360}{h}$倍.
点评 本题考查分式方程的应用,解答此类问题的关键是明确题意,列出相应的分式方程,注意分式方程要检验.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
10.已知抛物线y=ax2-2x+1与x轴有两个交点,那么a的取值范围是( )
| A. | a<1且a≠0 | B. | a>1且a≠2 | C. | a≥1且a≠2 | D. | a≤1且a≠0 |
7.一个电器商店卖出一件电器,售价为1820元,以进价计算,获利40%,则进价为( )
| A. | 728元 | B. | 1300元 | C. | 1092元 | D. | 455元 |
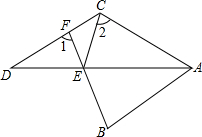 如图,AD平分∠BAC,∠BAC+∠ACD=180°,E在AD上,BE的延长线交CD于F,连CE,且∠1=∠2,求证:AB=AC.
如图,AD平分∠BAC,∠BAC+∠ACD=180°,E在AD上,BE的延长线交CD于F,连CE,且∠1=∠2,求证:AB=AC. 如图所示,可以用字母表示出来的不同射线有3条.
如图所示,可以用字母表示出来的不同射线有3条. 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,若△EDF的周长为9,则△BCF的周长为18.
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,若△EDF的周长为9,则△BCF的周长为18.