题目内容
4.两个不相等的实数a,b满足a2+b2=5.(1)若ab=2,求a+b的值;
(2)若a2-2a=m,b2-2b=m,求a+b和m的值.
分析 (1)先根据完全平方公式求出(a+b)2,再求出即可;
(2)两等式相加、相减,变形后求出a+b=2,再变形后代入a2+b2-2(a+b)=2m,即可求出m.
解答 解:(1)∵a2+b2=5,ab=2,
∴(a+b)2=a2+2ab+b2=5+2×2=9,
∴a+b=±3;
(2)∵a2-2a=m,b2-2b=m,
∴a2-2a=b2-2b,a2-2a+b2-2b=2m,
∴a2-b2-2(a-b)=0,
∴(a-b)(a+b-2)=0,
∵a≠b,
∴a+b-2=0,
∴a+b=2,
∵a2-2a+b2-2b=2m,
∴a2+b2-2(a+b)=2m,
∵a2+b2=5,
∴5-2×2=2m,
解得:m=$\frac{1}{2}$,
即a+b=2,m=$\frac{1}{2}$.
点评 本题考查了分解因式和完全平方公式等知识点,能灵活运用公式进行变形是解此题的关键.

练习册系列答案
相关题目
10.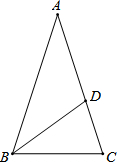 如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )
如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )
 如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )
如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )| A. | 30° | B. | 36° | C. | 45° | D. | 54° |
19.下列计算正确的是( )
| A. | $\sqrt{2}$$+\sqrt{2}$=2 | B. | 3+$\sqrt{2}$=3$\sqrt{2}$ | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | $\sqrt{9}$+$\sqrt{3}$=3$+\sqrt{3}$ |
16.要使分式$\frac{2x-3}{x-2}$的值存在(有意义),x的取值范围是( )
| A. | x=2 | B. | x≠2 | C. | $x=\frac{3}{2}$ | D. | $x≠\frac{3}{2}$ |
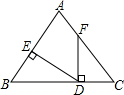 如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF=50°.
如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF=50°. 如图所示,可以用字母表示出来的不同射线有3条.
如图所示,可以用字母表示出来的不同射线有3条.