题目内容
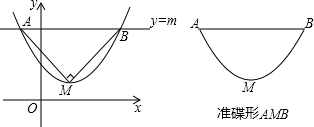
16.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a>0)的顶点为M,直线l与x轴平行,且与抛物线交于点A、B,若△AMB为等腰直角三角形,我们就把抛物线上A、B两点之间的部分与线段AB围成的图象称为该抛物线对应的“准蝶形”,线段AB的长称为碟宽,顶点M称为碟顶.(1)填空:抛物线y=x2的碟宽为2,碟顶坐标为(0,0);
(2)求抛物线y=a(x-2)2+3(a>0)的碟宽(用含a的代数式表示);
(3)若抛物线y=ax2-4ax-$\frac{5}{3}$(a>0)的碟宽为6,求该抛物线的碟顶坐标.
分析 (1)根据定义易算出含具体值的抛物线y=2x2的碟宽,利用端点(第一象限)横纵坐标的相等.推广至含字母的抛物线y=ax2(a>0),类似.而抛物线y=a(x-2)2+3(a>0)为顶点式,可看成y=ax2平移得到,则发现碟宽只和a有关.
(2)根据(1)的结论,根据碟宽易得关于a的方程$\frac{2}{a}$=6,解方程即可求得a的值.代入抛物线中得出解析式即可得出结论.
解答 解:(1)∵a>0,
∴y=ax2的图象大致如下: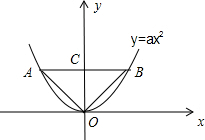
其必过原点O,记AB为其碟宽,AB与y轴的交点为C,连接OA,OB.
∵△OAB为等腰直角三角形,AB∥x轴,
∴OC⊥AB,
∴∠AOC=∠BOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×90°=45°,
∴△ACO与△BCO亦为等腰直角三角形,
∴AC=OC=BC,
∴xA=yA,xB=yB,代入y=ax2,
∴A(-$\frac{1}{a}$,$\frac{1}{a}$),B($\frac{1}{a}$,$\frac{1}{a}$),C(0,$\frac{1}{a}$),
∴AB=$\frac{2}{a}$,OC=$\frac{1}{a}$,
即y=ax2的碟宽为$\frac{2}{a}$.
∵抛物线y=x2对应的a=1,得碟宽$\frac{2}{a}$为2;碟顶(0,0),
故答案为:2,(0,0)
(2)由(1)知抛物线y=ax2(a>0),碟宽为$\frac{2}{a}$;
抛物线y=a(x-2)2+4(a>0)可看成y=ax2向右平移2个单位长度,再向上平移3个单位长度后得到的图形,
∵平移不改变形状、大小、方向,
∴抛物线y=a(x-2)2+3(a>0)与抛物线y=ax2的碟宽一样,
∵抛物线y=ax2(a>0),碟宽为$\frac{2}{a}$,
∴抛物线y=a(x-2)2+3(a>0),
碟宽为$\frac{2}{a}$.
(3)∵y=ax2-4ax-$\frac{5}{3}$=a(x-2)2-(4a+$\frac{5}{3}$),
∴同(1),其碟宽为$\frac{2}{a}$,
∵y=ax2-4ax-$\frac{5}{3}$的碟宽为6,
∴$\frac{2}{a}$=6,
解得a=$\frac{1}{3}$.
把a=$\frac{1}{3}$代入y=ax2-4ax-$\frac{5}{3}$=$\frac{1}{3}$x2-$\frac{4}{3}$x-$\frac{5}{3}$,
∴顶点坐标为(2,-3),
即:碟顶为(2,-3).
点评 本题考查二次函数综合题,题目中主要涉及特殊直角三角形,二次函数解析式与图象性质,解题的关键是由抛物线y=ax2(a>0),得到碟宽只和a有关,即碟宽$\frac{2}{a}$.

 名校课堂系列答案
名校课堂系列答案 如图,一条信息可通过网络线由上(A点)往下(沿箭头方向)向各站点传送,例如信息要到b2点可由经a1的站点送达,也可由经a2的站点送达,共有两条传送途径,则信息由A点传达到d3的不同途径中,经过站点b3的概率为( )
如图,一条信息可通过网络线由上(A点)往下(沿箭头方向)向各站点传送,例如信息要到b2点可由经a1的站点送达,也可由经a2的站点送达,共有两条传送途径,则信息由A点传达到d3的不同途径中,经过站点b3的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | 3$\sqrt{2}-\sqrt{2}$=2$\sqrt{2}$ | C. | 2$+\sqrt{2}=2\sqrt{2}$ | D. | $\sqrt{(-2)^{2}}$=±2 |
 如图,已知,∠BAC=35°,$\widehat{CD}$=80°,那么∠BOD的度数为( )
如图,已知,∠BAC=35°,$\widehat{CD}$=80°,那么∠BOD的度数为( )| A. | 75° | B. | 80° | C. | 135° | D. | 150° |
| A. | 1 | B. | -1 | C. | $\frac{1}{25}$ | D. | -$\frac{1}{25}$ |
| A. | mn>-9 | B. | -9≤mn≤0 | C. | -4≤mn≤0 | D. | mn≥-9且mn≠0 |
 已知长方形ABCO,A,C分别在x轴、y轴上,O是原点,点B(2,1),点D($\sqrt{3}$,0),将四边形ABCD沿折痕CD翻折.
已知长方形ABCO,A,C分别在x轴、y轴上,O是原点,点B(2,1),点D($\sqrt{3}$,0),将四边形ABCD沿折痕CD翻折. 如图.在△ABC中.已知CD是AB上的高,且CD=$\frac{1}{2}$AB.E,F分别是AC,BC的中点,求证:以EF为直径的⊙O与AB相切.
如图.在△ABC中.已知CD是AB上的高,且CD=$\frac{1}{2}$AB.E,F分别是AC,BC的中点,求证:以EF为直径的⊙O与AB相切.