题目内容
6. 如图.在△ABC中.已知CD是AB上的高,且CD=$\frac{1}{2}$AB.E,F分别是AC,BC的中点,求证:以EF为直径的⊙O与AB相切.
如图.在△ABC中.已知CD是AB上的高,且CD=$\frac{1}{2}$AB.E,F分别是AC,BC的中点,求证:以EF为直径的⊙O与AB相切.
分析 过O点作OH⊥AB于H,由E、F分别为AC、BC的中点,得到EF∥AB,且EF=$\frac{1}{2}$ AB,于是得到EF=CD证得OH=$\frac{1}{2}$EF,根据切线的判定定理即可得到结论.
解答 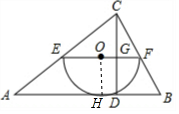 证明:过O点作OH⊥AB于H,
证明:过O点作OH⊥AB于H,
∵E、F分别为AC、BC的中点,
∴EF∥AB,且EF=$\frac{1}{2}$ AB,
∴G点为CD的中点,OH=GD=$\frac{1}{2}$CD,
∵CD=$\frac{1}{2}$AB,
∴EF=CD
∴OH=$\frac{1}{2}$EF,
∴AB为⊙O的切线.
点评 本题考查了切线的判定,三角形的中位线的性质,之前的作出辅助线是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
17.如果x个人y天做了a个零件,那么y个人用相同的速度做x个零件需要的天数是( )
| A. | $\frac{{x}^{2}}{a}$ | B. | $\frac{a}{{x}^{2}}$ | C. | $\frac{{a}^{2}}{x}$ | D. | $\frac{x}{{a}^{2}}$ |
14.如果-$\frac{1}{2}$a2b2n-1c是六次单项式,则n的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
16.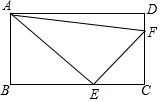 如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )
如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )
 如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )
如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )| A. | 3$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | $\sqrt{10}$ |
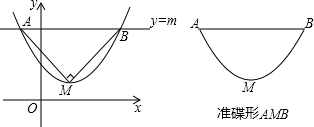
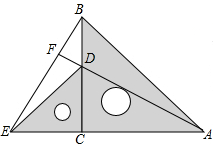 把两个含有45°角的大小不同的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.
把两个含有45°角的大小不同的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.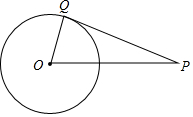 如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切
如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切