题目内容
5.若直线y=mx+6(m≠0)与双曲线y=$\frac{n}{x}$(n≠0)在第一象限有公共点,则( )| A. | mn>-9 | B. | -9≤mn≤0 | C. | -4≤mn≤0 | D. | mn≥-9且mn≠0 |
分析 依照题意画出图形,将一次函数解析式代入反比例函数解析式中,得出关于x的一元二次方程,由两者有交点,结合根的判别式即可得出结论.
解答 解:依照题意画出图形,如下图所示.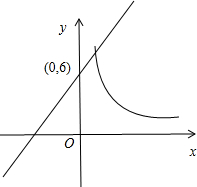
将y=mx+6代入y=$\frac{n}{x}$(n≠0)中,
得:mx+6=$\frac{n}{x}$,整理得:mx2+6x-n=0,
∵二者有交点,
∴△=62+4mn≥0,
∴mn≥-9.且mn≠0,
故选D.
点评 本题考查了反比例函数与一次函数的交点问题以及根的判别式,解题的关键由根的判别式得出关于mn的不等式.本题属于基础题,难度不大,解决该题型题目时,画出图形,利用数形结合解决问题是关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
15.已知x2-(2x+8)=0,则3x2-6(x+3)的值为( )
| A. | 54 | B. | 6 | C. | -10 | D. | -18 |
10.下列说法正确的是( )
| A. | “a是任意实数,则a2≥0”是随机事件 | |
| B. | 某彩票的中奖率为1%,则买100张彩票一定有1张会中奖 | |
| C. | 若某运动员投篮2次,投中1次,则该运动员投1次篮,投中的概率为$\frac{1}{2}$ | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
17.如果x个人y天做了a个零件,那么y个人用相同的速度做x个零件需要的天数是( )
| A. | $\frac{{x}^{2}}{a}$ | B. | $\frac{a}{{x}^{2}}$ | C. | $\frac{{a}^{2}}{x}$ | D. | $\frac{x}{{a}^{2}}$ |
14.如果-$\frac{1}{2}$a2b2n-1c是六次单项式,则n的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
 如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.
如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.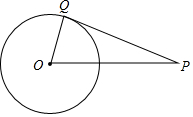 如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切
如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切