题目内容
11. 已知长方形ABCO,A,C分别在x轴、y轴上,O是原点,点B(2,1),点D($\sqrt{3}$,0),将四边形ABCD沿折痕CD翻折.
已知长方形ABCO,A,C分别在x轴、y轴上,O是原点,点B(2,1),点D($\sqrt{3}$,0),将四边形ABCD沿折痕CD翻折.(1)画出四边形ABCD翻折后的大致位置;
(2)求A、B两点翻折后的对应点A1,B1的坐标.
分析 (1)根据题意作出图形即可;
(2)根据矩形的性质得到OC=1,OD=$\sqrt{3}$,求得tan∠CDO=$\frac{OC}{OD}$=$\frac{\sqrt{3}}{3}$,得到∠CDO=30°,根据平角的定义得到∠CDA=150°,根据折叠的性质得到∠A1DC=150°,AD=A1D,得到△AA1D是等边三角形,解直角三角形得到结论.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)∵点B(2,1),点D($\sqrt{3}$,0),四边形ABCD是矩形,
∴OC=1,OD=$\sqrt{3}$,
∴tan∠CDO=$\frac{OC}{OD}$=$\frac{\sqrt{3}}{3}$,
∴∠CDO=30°,
∴∠BCD=30°,∠CDA=150°,
∵四边形ABCD沿折痕CD翻折,
∴∠A1DC=150°,AD=A1D,
∴△AA1D是等边三角形,
∴AD=2-$\sqrt{3}$,
∴A1(1+$\frac{\sqrt{3}}{2}$,$\sqrt{3}$-$\frac{3}{2}$),过B1作B1⊥y轴于E,
∵∠OCB1=30°,CB1=2,
∴CE=$\sqrt{3}$,B1E=1,
∴B1(1,$\sqrt{3}$-1).
点评 本题考查了矩形的性质,折叠的性质,坐标与图形的性质,等边三角形的判定和性质,解直角三角形,之前的作出图形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

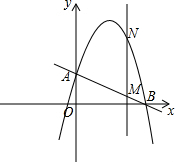 如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.
如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.