题目内容
8.数轴上点A表示的数a与点B表示的数b满足(a+7)2+|b-6|=0.(1)a=-7;b=6
(2)若点A现在以每秒2个单位的速度沿着数轴向右运动,点B同时沿着数轴以每秒3个单位的速度向左运动则t秒后点A表示的数是-7+2t,点B表示的数是6-3t,点A与点B之间的距离AB=13-5t或5t-13.(用含t的代数式表示)
(3)在(2)的条件下,点A和点B运动多久后相距1个单位长度.
分析 (1)根据非负数性质可得;
(2)由向右即为加上运动距离,向左即为减去运动距离可得A、B所表示的数,根据两点间距离公式分类讨论即可;
(3)利用(2)的结果解方程可得.
解答 解:(1)∵(a+7)2+|b-6|=0,
∴a+7=0,且b-6=0,即a=-7,b=6;
故答案为:-7,6;
(2)根据题意知,t秒后点A表示的数是-7+2t,点B表示的数为6-3t,
若点A在点B的左侧,则AB 间的距离为6-3t-(-7+2t)=13-5t,
若点A在点B的右侧,则AB间的距离为(-7+2t)-(6-3t)=-13+5t,
故答案为:-7+2t,6-3t,13-5t或5t-13;
(3)由(2)知,若13-5t=1,解得t=2.4,
若5t-13=1,解得t=2.8,
答:点A和点B运动2.4秒或2.8秒后相距1个单位长度.
点评 本题主要考查列代数式、非负数性质、两点间距离公式等知识点,掌握两点间距离公式并分类讨论是关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
18.从2,3,4,5这四个数中,任取两个数p和q(p≠q),构成函数y=px-2和y=x+q,若两个函数图象的交点在直线x=2的左侧,则这样的有序数组(p,q)共有( )
| A. | 12组 | B. | 10组 | C. | 6组 | D. | 5组 |
17.如果x个人y天做了a个零件,那么y个人用相同的速度做x个零件需要的天数是( )
| A. | $\frac{{x}^{2}}{a}$ | B. | $\frac{a}{{x}^{2}}$ | C. | $\frac{{a}^{2}}{x}$ | D. | $\frac{x}{{a}^{2}}$ |

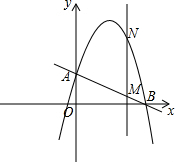 如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.
如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点. 如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.
如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.