题目内容
4.现规定:|$\begin{array}{l}a&b\\ c&d\end{array}$|=a-b+c-d,则|$\begin{array}{l}{xy-3{x^2}}&{-2xy-{x^2}}\\{-2{x^2}-3}&{-5+xy}\end{array}$|=2xy-4x2+2.分析 首先根据例题可得|$\begin{array}{l}{xy-3{x^2}}&{-2xy-{x^2}}\\{-2{x^2}-3}&{-5+xy}\end{array}$|=(xy-3x2)-(-2xy-x2)+(-2x2-3)-(-5+xy),然后再去括号,合并同类项即可.
解答 解:∵|$\begin{array}{l}a&b\\ c&d\end{array}$|=a-b+c-d,
∴|$\begin{array}{l}{xy-3{x^2}}&{-2xy-{x^2}}\\{-2{x^2}-3}&{-5+xy}\end{array}$|
=(xy-3x2)-(-2xy-x2)+(-2x2-3)-(-5+xy)
=xy-3x2+2xy+x2-2x2-3+5-xy
=2xy-4x2+2.
故答案为:2xy-4x2+2.
点评 此题主要考查了整式的加减,关键是弄懂例题含义,列出式子.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,若A(4,0),B(2,2),则点D的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,若A(4,0),B(2,2),则点D的坐标为( )
 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,若A(4,0),B(2,2),则点D的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,若A(4,0),B(2,2),则点D的坐标为( )| A. | (1,2) | B. | (1,1) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | (2,1) |
13.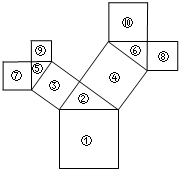 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,如果用S1表示正方形①的面积,用S2表示直角三角形②的面积,…,依次将这些正方形和直角三角形的面积分别用S1,S2,…,S10表示出来,有以下等式:
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,如果用S1表示正方形①的面积,用S2表示直角三角形②的面积,…,依次将这些正方形和直角三角形的面积分别用S1,S2,…,S10表示出来,有以下等式:
①S1=S3+S4; ②S1=S3+S7+S9;
③S1=S4+S7+S9; ④S1=S7+S8+S9+S10
其中一定成立的有( )
 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,如果用S1表示正方形①的面积,用S2表示直角三角形②的面积,…,依次将这些正方形和直角三角形的面积分别用S1,S2,…,S10表示出来,有以下等式:
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,如果用S1表示正方形①的面积,用S2表示直角三角形②的面积,…,依次将这些正方形和直角三角形的面积分别用S1,S2,…,S10表示出来,有以下等式:①S1=S3+S4; ②S1=S3+S7+S9;
③S1=S4+S7+S9; ④S1=S7+S8+S9+S10
其中一定成立的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
14.下列计算正确的是( )
| A. | $\sqrt{(-3)^{2}}=-3$ | B. | $\sqrt{\frac{2}{3}}=\frac{1}{3}\sqrt{2}$ | C. | $\frac{1}{2-\sqrt{3}}=2+\sqrt{3}$ | D. | 5-3$\sqrt{2}$=2$\sqrt{2}$ |
