题目内容
18.已知菱形的一个内角为120°,且平分这个内角的对角线长为9cm,则这个菱形的周长为( )| A. | 18 | B. | 72 | C. | 36 | D. | 54 |
分析 先证明△ABD是等边三角形,得出AB=AD=BD=9cm,即可求出菱形的周长.
解答 解:如图所示: ∵四边形ABCD是菱形,∠ADC=120°,
∵四边形ABCD是菱形,∠ADC=120°,
∴AB=AD=BC=CD,∠ADB=60°,
∴△ABD是等边三角形,
∴AB=AD=BD=9cm,
∴菱形ABCD是周长为9÷=36(cm);
故选:C.
点评 本题考查了菱形的性质以及等边三角形的判定与性质;证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
7.下列各式从左到右的变形正确的是( )
| A. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | B. | $\frac{0.2a+b}{a+0.2b}$=$\frac{2a+b}{a+2b}$ | ||
| C. | -$\frac{x+1}{x-y}$=$\frac{x-1}{x-y}$ | D. | $\frac{x-\frac{1}{2}y}{\frac{1}{2}x+y}$=$\frac{2x-y}{x+2y}$ |
8.底面半径R,高为h的圆柱与底面半径为r,高为h的圆柱的体积的比是9:25,则R:r等于( )
| A. | 9:25 | B. | 25:9 | C. | 3:5 | D. | 5:3 |
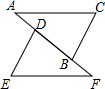 如图,已知AD=FB,AC∥EF,∠C=∠E,点A,D,B,F在一条直线上.请判定AC与EF的大小关系,并证明你的结论.
如图,已知AD=FB,AC∥EF,∠C=∠E,点A,D,B,F在一条直线上.请判定AC与EF的大小关系,并证明你的结论.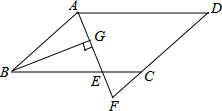 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G.若BG=$4\sqrt{2}$,则△CEF的面积是2$\sqrt{2}$.
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G.若BG=$4\sqrt{2}$,则△CEF的面积是2$\sqrt{2}$.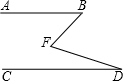 如图,已知AB∥CD,证明:∠BFD=∠B+∠D.(用两种方法证明)
如图,已知AB∥CD,证明:∠BFD=∠B+∠D.(用两种方法证明)