题目内容
8.下面的三个大三角形中各有三个小三角形,每个大三角形中的四个数都有规律,请按左、右每个大三角形内填数的规律,在中间的大三角形的中间“?”处填上恰当的数是$\sqrt{432}$.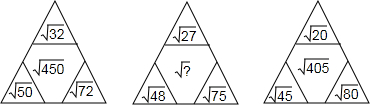
分析 化简后可知:$\sqrt{450}$(15$\sqrt{2}$)=$\sqrt{32}$+$\sqrt{50}$+$\sqrt{72}$=4$\sqrt{2}$+5$\sqrt{2}$+6$\sqrt{2}$;$\sqrt{405}$(9$\sqrt{5}$)=$\sqrt{20}$+$\sqrt{45}$+$\sqrt{80}$=2$\sqrt{5}$+3$\sqrt{5}$+4$\sqrt{5}$,由此得出三角形中间的数等于三个顶点的数字和,由此规律得出答案即可.
解答 解:$\sqrt{?}$=$\sqrt{27}$+$\sqrt{48}$+$\sqrt{75}$=3$\sqrt{3}$+4$\sqrt{3}$+5$\sqrt{3}$=12$\sqrt{3}$=$\sqrt{432}$.
故答案为:$\sqrt{432}$.
点评 此题考查数字的变化规律,找出数字之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知菱形的一个内角为120°,且平分这个内角的对角线长为9cm,则这个菱形的周长为( )
| A. | 18 | B. | 72 | C. | 36 | D. | 54 |
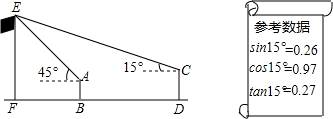
 如图所示,小明、小军、小丽三个同学家正好住在一个小区,小军和小丽家在同一栋楼AE里,高度相差AB为(42+14$\sqrt{3}$)米,小明家在他们相对的一栋楼CD上,一日,小明站在自家阳台C处,发现小军家住A处,且仰角为45°,而小丽家在B处,俯角为30°,小丽家离地面高度BE=6米,试求两栋楼之间的距离DE及小明家离地面的高度CD($\sqrt{3}$=1.73,结果精确到0.01)
如图所示,小明、小军、小丽三个同学家正好住在一个小区,小军和小丽家在同一栋楼AE里,高度相差AB为(42+14$\sqrt{3}$)米,小明家在他们相对的一栋楼CD上,一日,小明站在自家阳台C处,发现小军家住A处,且仰角为45°,而小丽家在B处,俯角为30°,小丽家离地面高度BE=6米,试求两栋楼之间的距离DE及小明家离地面的高度CD($\sqrt{3}$=1.73,结果精确到0.01)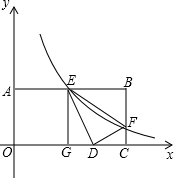 如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$.
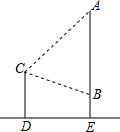
如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$. 如图,已知△ABC,点D,过点D作△ABC平移后的图形△DEF,使点A移动到点D.(其中点B与点E是对应点,点C与点F是对应点)
如图,已知△ABC,点D,过点D作△ABC平移后的图形△DEF,使点A移动到点D.(其中点B与点E是对应点,点C与点F是对应点)