题目内容
18.(1)计算:(-$\frac{1}{2}$)-2-|$\sqrt{3}$-1|+(-$\sqrt{3}$+1)0+3tan30°(2)解方程:$\frac{x}{x-1}$+$\frac{2}{1-x}$=4.
分析 (1)原式利用零指数幂,负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=4-$\sqrt{3}$+1+1+$\sqrt{3}$=6;
(2)去分母得:x-2=4(x-1),
解得:x=$\frac{2}{3}$,
经检验x=$\frac{2}{3}$是分式方程的解.
点评 此题考查了解分式方程,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
七年级兴趣班报名情况统计表.
(1)报名参加兴趣班的总人数为80人;统计表中的a=0.3;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?
 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:七年级兴趣班报名情况统计表.
| 兴趣班名称 | 频率 |
| “无人机” | a |
| “3D打印” | 0.05 |
| “网页设计” | 0.25 |
| “电脑绘画” | 0.40 |
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?
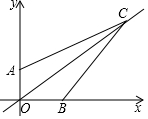 如图,已知点A(0,3),B(4,0),点C在第一象限,且AC=5$\sqrt{5}$,BC=10,则直线OC的函数表达式为y=$\frac{4}{5}$x.
如图,已知点A(0,3),B(4,0),点C在第一象限,且AC=5$\sqrt{5}$,BC=10,则直线OC的函数表达式为y=$\frac{4}{5}$x.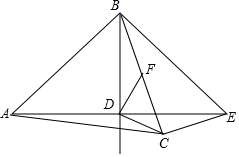 如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.