题目内容
13.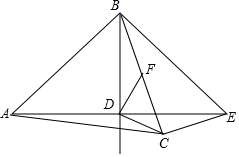 如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.(1)若BD=DE=$\sqrt{5}$,CE=$\sqrt{2}$,求BC的长;
(2)若BD=DE,求证:BF=CF.
分析 (1)利用勾股定理求出BE的长,进而再次利用勾股定理求出BC的长;
(2)连接AF,首先利用ASA证明出△BDF≌△EDC,得到DF=CD,进而得到∠ADF=∠BDC,再次利用SAS证出△ADF≌△BDC,结合题干条件得到AF⊥BC,利用等腰三角形的性质得到结论.
解答 解:(1)∵BD⊥AD,点E在AD的延长线上,
∴∠BDE=90°,
∵BD=DE=$\sqrt{5}$,
∴BE=$\sqrt{B{D}^{2}+D{E}^{2}}$=$\sqrt{10}$,
∵BC⊥CE,
∴∠BCE=90°,
∴BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=$\sqrt{10-2}$=2$\sqrt{2}$;
(2)连接AF,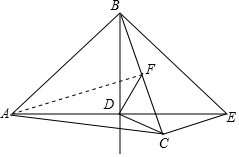
∵CD⊥BD,DF⊥CD,
∴∠BDE=∠CDF=90°,
∴∠BDF=∠CDE,
∵CE⊥BC,
∴∠BCE=90°,
∴∠DBC=∠CED,
在△BDF和△EDC中,
∵$\left\{\begin{array}{l}{∠DBF=∠DEC}\\{BD=DE}\\{∠BDF=∠CDE}\end{array}\right.$,
∴△BDF≌△EDC(ASA),
∴DF=CD,
∴∠CFD=∠DCF=45°,
∵∠ADB=∠CDF,
∴∠ADB+∠BDF=∠CDF+∠BDF,
∴∠ADF=∠BDC,
在△ADF和△BDC中,
∵$\left\{\begin{array}{l}{AD=BD}\\{∠ADF=∠BDC}\\{DF=CD}\end{array}\right.$,
∴△ADF≌△BDC(SAS),
∴∠AFD=∠BCD,
∴∠AFD=45°,
∴∠AFC=∠AFD+∠CFD=90°,
∴AF⊥BC,
∴AB=AC,
∴BF=CF.
点评 本题主要考查了全等三角形的判定与性质,解题的关键是熟练掌握全等三角形的判定方法,特别是第二问需要利用ASA和SAS证明三角形全等,此题有一定的难度.

 通城学典默写能手系列答案
通城学典默写能手系列答案| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 平均成绩 | |
| 甲 | 7 | ▲ | 8 | 10 | 8 | 8 |
| 乙 | 7 | 8 | 8 | 9 | 8 | ▲ |
| A. | 甲运动员的第2次射击成绩为7环 | B. | 乙运动员的平均射击成绩为8环 | ||
| C. | 甲运动员这5次射击成绩的方差为6 | D. | 乙运动员的成绩更稳定 |