题目内容
17.规定运算:对于函数y=xn(n为正整数),规定y′=nxn-1.例如:对于函数y=x4,有y′=4x3.已知函数y=x3,满足y′=18的x的值为( )| A. | x1=3,x2=-3 | B. | x1=x2=0 | C. | x1=$\sqrt{6}$,x2=-$\sqrt{6}$ | D. | x1=3$\sqrt{2}$,x2=-3 |
分析 根据新定义得到3x2=18,然后利用直接开平方法解方程即可.
解答 解:根据题意得3x2=18,
即x2=6,
所以x1=$\sqrt{6}$,x2=-$\sqrt{6}$.
故选C.
点评 本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.也考查了阅读理解能力.

练习册系列答案
相关题目
5.在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,那么$\overrightarrow{BC}$等于( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-$\overrightarrow{b}$ | C. | -$\overrightarrow{a}$+$\overrightarrow{b}$ | D. | -$\overrightarrow{a}$-$\overrightarrow{b}$ |
6.下列运算正确的是( )
| A. | x3÷x2=x | B. | x3•x2=x6 | C. | x3-x2=x | D. | x3+x2=x5 |
2.如图是魔术师在小颖面前表演的经过,小颖任意写了一个数字m,那么魔术师猜中的运算结果应为( )

| A. | 2 | B. | 3 | C. | 6 | D. | m+3 |
9.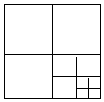 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
 连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )
连结边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2017次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2017}$ | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{1}{4}$)2017 | D. | 1-($\frac{1}{4}$)2017 |
 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.则BC、EF的位置关系为平行.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.则BC、EF的位置关系为平行. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=16,CD=6,则AC=12.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D.若BC=16,CD=6,则AC=12.