题目内容
14.现有三张反面朝上的扑克牌:红桃2、红桃3、黑桃x(1≤x≤13且x为奇数或偶数).把牌洗匀后第一次抽取一张,记好花色和数字后将牌放回,重新洗匀第二次再抽取一张.(1)求两次抽得相同花色的概率;
(2)当甲选择x为奇数,乙选择x为偶数时,他们两次抽得的数字和是奇数的可能性大小一样吗?请说明理由.(提示:三张扑克牌可以分别简记为红2、红3、黑x)
分析 (1)如图,根据树状图求出所有可能的结果有9种,两次抽得相同花色的可能性有5种,即可得到结果;
(2)根据树状图求出两次抽得的数字和是奇数的可能性再分别求出他们两次抽得的数字和是奇数的概率比较即可.
解答  解:(1)如图,所有可能的结果有9种,两次抽得相同花色的可能性有5种,
解:(1)如图,所有可能的结果有9种,两次抽得相同花色的可能性有5种,
∴P(相同花色)=$\frac{5}{9}$,
∴两次抽得相同花色的概率为:$\frac{5}{9}$;
(2)他们两次抽得的数字和是奇数的可能性大小一样,
∵x为奇数,两次抽得的数字和是奇数的可能性有4种,
∴P(甲)=$\frac{4}{9}$,
∵x为偶数,两次抽得的数字和是奇数的可能性有4种,
∴P(乙)=$\frac{4}{9}$,
∴P(甲)=P(乙),
∴他们两次抽得的数字和是奇数的可能性大小一样.
点评 本题考查了树状图法求概率,解决这类题的关键是正确的画出树状图.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
4. 如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
 如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75°方向20米处,点C在点A南偏西15°方向20米处,则点B与点C的距离为20$\sqrt{2}$米.
19.如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是( )


| A. | 240πcm2 | B. | 480πcm2 | C. | 1200πcm2 | D. | 2400πcm2 |
3.某种蔬菜按品质分成三个等级销售,销售情况如表:
则售出蔬菜的平均单价为4.4元/千克.
| 等级 | 单价(元/千克) | 销售量(千克) |
| 一等 | 5.0 | 20 |
| 二等 | 4.5 | 40 |
| 三等 | 4.0 | 40 |
 在△ABC中,∠ACB=90°,AC=BC=2,M是边AC的中点,CH⊥BM于H.
在△ABC中,∠ACB=90°,AC=BC=2,M是边AC的中点,CH⊥BM于H.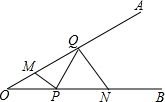 如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是$\sqrt{10}$.
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是$\sqrt{10}$.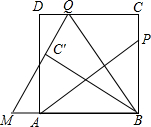 如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.