题目内容
15. 如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
分析 过P作PM⊥AB于M,求出∠PBM=45°,∠PAM=30°,求出PM,即可求出BM、BP.
解答  解:如图:
解:如图:
过P作PM⊥AB于M,
则∠PMB=∠PMA=90°,
∵∠PBM=90°-45°=45°,∠PAM=90°-60°=30°,AP=20海里,
∴PM=$\frac{1}{2}$AP=10海里,AM=cos30°AP=10$\sqrt{3}$海里,
∴∠BPM=∠PBM=45°,
∴PM=BM=10海里,
∴AB=AM+BM=(10+10$\sqrt{3}$)海里,
∴BP=$\frac{PM}{sin45°}$=10$\sqrt{2}$海里,
即小船到B码头的距离是10$\sqrt{2}$海里,A、B两个码头间的距离是(10+10$\sqrt{3}$)海里.
点评 本题考查了解直角三角形,含30度角的直角三角形性质的应用,能正确解直角三角形是解此题的关键,难度适中.

练习册系列答案
相关题目
3.某种蔬菜按品质分成三个等级销售,销售情况如表:
则售出蔬菜的平均单价为4.4元/千克.
| 等级 | 单价(元/千克) | 销售量(千克) |
| 一等 | 5.0 | 20 |
| 二等 | 4.5 | 40 |
| 三等 | 4.0 | 40 |
 在△ABC中,∠ACB=90°,AC=BC=2,M是边AC的中点,CH⊥BM于H.
在△ABC中,∠ACB=90°,AC=BC=2,M是边AC的中点,CH⊥BM于H.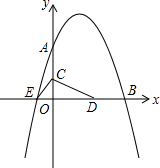 如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动. 如图所示的几何体是由五个小正方体组合而成的,它的主视图是( )
如图所示的几何体是由五个小正方体组合而成的,它的主视图是( )



 如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?
如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?