题目内容
1.已知函数y=x-1与y=$\frac{6}{x}$图象的交点为A、B,y轴上有一点P,到原点距离为4.则△PAB的面积为为$\frac{25}{2}$或$\frac{15}{2}$.分析 联立方程求得交点坐标,求得直线与y轴的交点C坐标,进而求得PC的长,然后根据S△PAB=S△PAC+S△PBC即可求得.
解答 解:∵函数y=x-1与y=$\frac{6}{x}$图象的交点为A、B,
∴$\left\{\begin{array}{l}{y=x-1}\\{y=\frac{6}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$,
∴A(3,2),B(-2,-3),
由直线y=x-1可知,直线与y轴的交点C为(0,-1),
∵P到原点距离为4,
∴PC=5或3,
当PC=5时,则S△PAB=S△PAC+S△PBC=$\frac{1}{2}$×5×2+$\frac{1}{2}$×5×3=$\frac{25}{2}$;
当PC=3时,则S△PAB=S△PAC+S△PBC=$\frac{1}{2}$×3×2+$\frac{1}{2}$×3×3=$\frac{15}{2}$.
故答案为$\frac{25}{2}$或$\frac{15}{2}$.
点评 本题考查了反比例函数和一次函数的交点问题,求得直线与y轴的交点是解题的关键,注意P点有两种情况.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
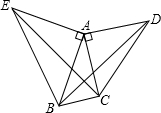 如图,△ACD,△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,画出△ACE以点A为旋转中心,逆时针方向旋转90°后的三角形,判断CE与BD的位置关系.
如图,△ACD,△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,画出△ACE以点A为旋转中心,逆时针方向旋转90°后的三角形,判断CE与BD的位置关系.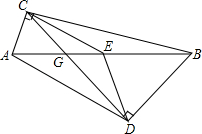 如图,△ABC,△ABD都是直角三角形,∠BDA,∠BCA都是直角,E为斜边AB的中点,点C,D的连结线与AB相交于点G,CE=DE,∠ABC=20°,∠ABD=50°,求∠AGC的度数.
如图,△ABC,△ABD都是直角三角形,∠BDA,∠BCA都是直角,E为斜边AB的中点,点C,D的连结线与AB相交于点G,CE=DE,∠ABC=20°,∠ABD=50°,求∠AGC的度数.