题目内容
20.如图是用棋子摆成的“小徽标”:
摆第1个图形需要4个棋子,摆第2个图形需要9个棋子,摆第3个图形需要14个棋子,按照这样的方式继续摆下去,则摆第n个图形需要(5n-1)个棋子.
分析 当n=1、n=2、n=3、n=4时,图形棋子个数分别是1+2+1=4=5-1、1+2+3+2+1=9=2×5-1、2+3+4+3+2=14=3×5-1、3+4+5+4+3=19=4×5-1…,运用不完全归纳法不难得出结论.
解答 解:当n=1时,棋子的个数:1+2+1=4=5-1,
当n=2时,棋子的个数:1+2+3+2+1=9=2×5-1,
当n=3时,棋子的个数:2+3+4+3+2=14=3×5-1,
当n=4时,棋子的个数:3+4+5+4+3=19=4×5-1,
…
第n个图形,棋子的个数:5n-1.
故答案为:(5n-1).
点评 本题考查了规律型:图形的变化,关键是通过归纳与总结,得到其中的规律.注意由特殊到一般的分析方法,本题从屋顶和屋身两部分寻找规律.

练习册系列答案
相关题目
11.有下列四种说法:
(1)过直线外一点有且只有一条直线与这条直线平行
(2)平面内,过一点能且只能作一条直线与已知直线垂直
(3)直线外一点与直线上各点连接的所有线段中,垂线段最短
(4)平行于同一条直线的两条直线平行.
其中正确的个数是( )
(1)过直线外一点有且只有一条直线与这条直线平行
(2)平面内,过一点能且只能作一条直线与已知直线垂直
(3)直线外一点与直线上各点连接的所有线段中,垂线段最短
(4)平行于同一条直线的两条直线平行.
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.我国四部地区约占我国国土面积的$\frac{2}{3}$,我国国土面积约960万平方公里.若用科学记数法表示,则我国四部地区的面积是( )
| A. | 6.4×107平方公里 | B. | 6.4×106平方公里 | C. | 64×105平方公里 | D. | 640×104平方公里 |
10.若多项式x4+mx3+nx-16含有因式(x-2)和(x-1),则mn的值是( )
| A. | 100 | B. | 0 | C. | -100 | D. | 50 |

 如图,直线AB,CD被BC所截,E是BC上一点,连接DE.若AB∥CD,∠1=45°,∠2=35°,则∠3=80度.
如图,直线AB,CD被BC所截,E是BC上一点,连接DE.若AB∥CD,∠1=45°,∠2=35°,则∠3=80度.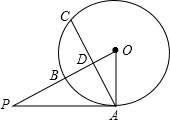 如图,已知PA为⊙O的切线,点A为切点,PO交⊙O于点B,点C是⊙O上一点,且$\widehat{AB}$=$\widehat{BC}$,PO交AC于点D,若PA=2$\sqrt{6}$,OD=2,求⊙O的半径和BD的长.
如图,已知PA为⊙O的切线,点A为切点,PO交⊙O于点B,点C是⊙O上一点,且$\widehat{AB}$=$\widehat{BC}$,PO交AC于点D,若PA=2$\sqrt{6}$,OD=2,求⊙O的半径和BD的长.